Um canal retangular tem 2 m de largura e contém água com 3 m de profundidade. Se a declividade for de 0,85° e o revestimento for de metal corrugado, calcule o valor da descarga para escoamento uniforme.
Passo 1
Vamos esquematizar a seção dessa canal para entendermos melhor o que está acontecendo:
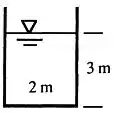
Neste exercício, precisamos calcular a “desacarga” ou simplesmente a vazão do canal.
Vimos nessa teoria que a velocidade é
Vamos então calcular o raio hidráulico a declividade e a componente de atrito do metal corrugado e então lembrar daquela fórmula clássica:
Passo 2
Vamos começar pelo mais chatinho que é calcular o raio hidráulico:
Que é a área da seção sobre o perímetro molhado:
Logo :
Passo 3
O atrito que vamos utilizar na fórmula da velocidade é o do metal corrugado, olhando aquela tabelinha que forneci na teoria, o número de Manning é de:
E sabemos também que
Aplicando na fórmula da velocidade:
Multiplicando pela área temos a vazão
Resposta
A descarga é de .