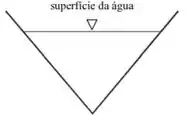
A partir da figura acima, que ilustra a seção transversal de um canal triangular aberto, assinale a opção correta acerca de hidráulica aplicada em canais abertos.

(A) O perímetro molhado corresponde ao resultado da soma dos comprimentos das faces em contato com a água com o comprimento da superfície da água

(B) O raio hidráulico corresponde ao comprimento de uma das faces do canal em contato com a água

(C) A profundidade de escoamento equivale à distância vertical entre o vértice no fundo do canal e a superfície da água.

(D) A borda livre deve ser considerada no cálculo do perímetro molhado.

(E) A velocidade máxima da água em canais desse tipo ocorre no vértice inferior do canal triangular

E aí, jovem mestre! Vamos relembrar o que aprendemos na teoria. O perímetro molhado é a soma dos lados do canal que são molhados pelo fluido.

É justamennto por isso que sua definição não inclui a superfície da água ou borda livre. Logo, as afirmações A e D estão erradas.

Vimos na teoria que o radio hidráulico é esse carinha aqui:

Ou seja, o raio hidráulico é a área dividida pelo perímetro molhado, ou simplesmente, um quarto do diâmetro hidráulico. Analisando essa definição, não podemos dizer que o raio hidráulico corresponde ao comprimento de uma das faces do canal em contato com a água...

Logo, a afirmação B também está errada.

A letra C diz que a profundidade de escoamento é a distância vertical entre o vértice no fundo do canal e a superfície da água. Como esse vértice é o ponto mais profundo do canal, essa afirmação é verdadeira e a resposta é a letra C :D

Antes de terminar, vamos ver por que a E não está certa. No vértice inferior do canal triangular mostrado, a velocidade do fluido é a velocidade do canal pela condição de não-deslizamento.

Geralmente essa velocidade no fundo é zero, pois o canal costuma estar parado. Logo, a velocidade máxima não fica no fundo e a letra E está errada.

A afirmação C é a única verdadeira dentre essas 5.