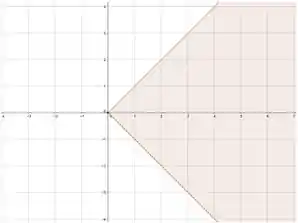
Determine e esboce o domínio de
Passo 1
A gente precisa achar o domínio e esboça-lo, vamos por partes então! Começando por colocar os nossos passos em ação!
Vendo a nossa função com atenção, podemos destacar dois casos que interferem no domínio:
1-Dentro das raízes de índice par não pode ter número menor que (não pode ser um número negativo);
2-O denominador da fração não pode ser .
Passo 2
Agora podemos estabelecer as restrições da função.
Se dentro das raízes pares não pode ter número menor que , então, na nossa função
Vamos separar em partes! A primeira é essa aqui:
Como é uma raiz ímpar, não temos restrição nenhuma! A problema é só quando é par, ok?
Agora para
temos uma raiz par, então precisamos que
Passando o para o outro lado, ficamos com
Que podemos escrever assim:
Vamos guardar isso, que já já vamos precisar!
Passo 3
Agora para nossa última parte da função temos que o denominador da fração não pode ser
Logo,
Maaaas não acabamos por aí, percebe aqui comigo o denominador também é uma raiz par, então além de ser ele tambem tem que ser maior que zero.
Então vamos atualizar o resultado que encontramos no passo 2. Fica, então
Juntando as duas condições temos que
Porque não pode negativo, nem igual a zero. Por isso que o sinal de se transformou em apenas .
Assim:
Show, agora vamos desenhar isso.
Passo 4
Mas agora como que você descobre o que essa desigualdade representa no plano? Basta fingir que é uma igualdade!
Assim:
Se transforma em:
E o gráfico é esse aqui:
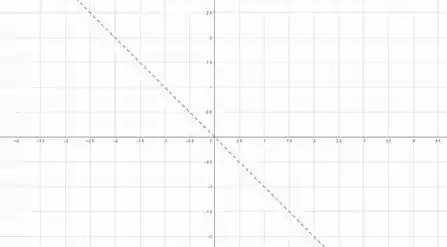
Agora vamos colocar o sinal correto que é:
Ou seja, essa parte do domínio é tudo à direita da reta , excluindo a reta (porque o sinal é só de “maior que”, e não de “maior ou igual”). Encontramos isso:
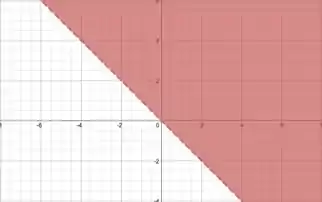
Show, essa parte foi.
Mas lembra do que encontramos lá no passo 2, quando fizemos
Achamos:
Vamos trocar o sinal também, colocando uma igualdade pra ajudar a gente a começar a desenhar essa parte. Agora teremos a reta . Que nos dá esse gráfico aqui:
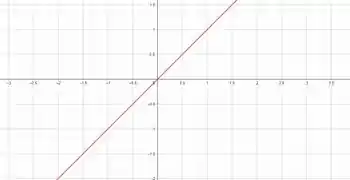
Voltando para o sinal certo, temos:
E como o sinal é de menor ou igual, a reta está inclusa, é pegamos tudo à sua direita. Fica assim:
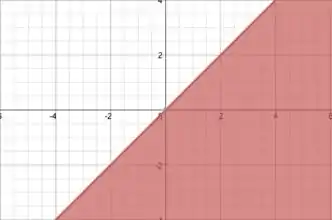
Passo 5
Pra gente esboçar o domínio todo é só sobrepor os que já temos! Fica assim:

Prontinho, nosso domínio está representado pela parte mais escura do gráfico.
Resposta
O domínio é dado por que é a interseção de e .
E seu esboço é: