Determine e faça o esboço do domínio da função:

Agora é só trabalhar em cima da expressão encontrada, e ver que curva ela representa:

Passando para o outro lado ficamos com

“Hmmm ainda não estou conseguindo visualizar direito o que pode ser isso”, quando isso acontece a gente costuma a dividir os dois lados pelo número que ficou sozinho, ficamos com:

E a gente pode cortar os ’s e nas frações de e , ficando com

Percebe que a inequação é muito parecida com a equação de um elipsoide? Não lembra da equação do elipsoide, não tem problema! Olha ela aqui:

E encontramos

Como na equação do elipsoide, os denominadores estão elevados ao quadrado, vamos escrever nossa inequação assim também:

Ou seja, nosso , e ! E o sinal de “menor que” que nos dizer que a função existe apenas para pontos dentro do elipsoide.

Por exemplo, se pegarmos um ponto que esteja fora dele, acharemos um valor maior do que , o que torna a inequação falsa!

Legal, temos o nosso domínio, agora, como esboçá-lo? Para isso podemos anular uma das variáveis e encontrar a curva no plano formado pelas outras duas.

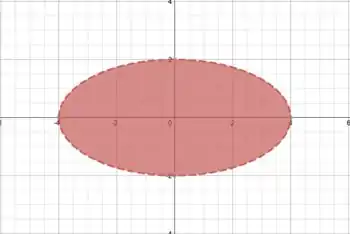
Por exemplo, anulando a variável , ou seja, fazendo , teremos:

Que representa uma elipse no plano , com seu interior preenchido (pelo sinal de “menor que”)

Agora, fazendo o mesmo para ,fazendo , temos a curva projetada no plano :

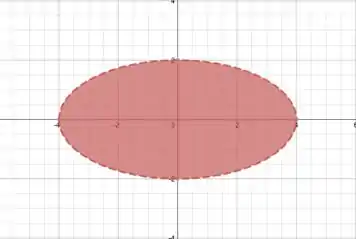
Perceba que é uma outra elipse, exatamente como a primeira, mas em outro plano!

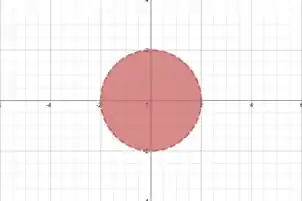
Finalmente, anulando a variável , encontramos com que

Que é a equação de uma circunferência no plano , pois os denominadores de e possuem o mesmo valor!

Juntando as curvas com interior preenchido que encontramos, temos como esboçar o elipsoide! Basta desenhar cada umas dessas curvas em seus respectivos plano, e depois completar com as linhas que formariam o sólido. A gente fica com isso aqui:

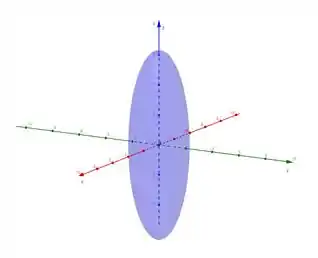
Tudo que está dentro desse elipsoide é nosso domínio! Muito doido né? :P