Seja
a) Esboce a curva de nível de que corresponde ao nível . Em que pontos essa curva intercepta o eixo ?
Passo 1
Opaa, vamos continuar nossos estudos aqui que a gente tá na reta final!
Ok, ele quer a curva de nível que tem . Então, tudo o que temos que fazer é pegar a função e igualá-la a :
E agora partiu ver que curva é essa! Vamos desenvolver melhor essa equação?
Passando o denominador multiplicando para o outro lado, temos:
Fazendo essa distributiva, ficamos com
Dividindo tudo por , vamos ter:
Passo 2
Agora, o que acha de completarmos o quadrado para o ? Vamos pensar num produto notável com . Vamos pensar aqui:
Uhul, vamos adicionar e subtrair na nossa equação, ficando com:
Vamos dividir tudo por para ficar com do outro lado! Temos então:
E pronto! Temos aí a equação de uma elipse, centrada em !
Passo 3
Agora, analisemos o que o enunciado realmente pediu: em que ponto essa curva corta o eixo ? Para saber disso, temos que fazer , e então teremos o ponto pedido :)
Tirando a raiz quadrada dos dois lados,
Isso dá pra gente isso aqui:
Passo 4
Mas tome muito cuidado agora!
Encontramos os pontos e , certo? Não!
Temos apenas o segundo, pois a origem não faz parte do domínio da função! Isso porque substituindo os valores na função temos uma divisão por zero.
Assim, temos apenas o ponto , pois a curva não toca a origem:
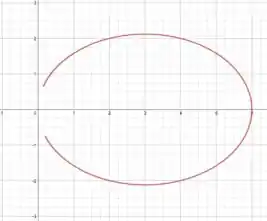
Passo 5
Coloquei direto a imagem da elipse, mas se você tiver alguma dúvida de como se esboça, é só lembrar da equação geral:
Então, como nosso e , seu centro está em . Aí para ver os semieixos, você pega, a partir do centro, e na direção e e na direção !
Resposta
a) Corta o eixo no ponto , apenas.