Exercícios Resolvidos de Introdução às Funções de Várias Variáveis, Curvas de Nível
Ver TeoriaEnunciado
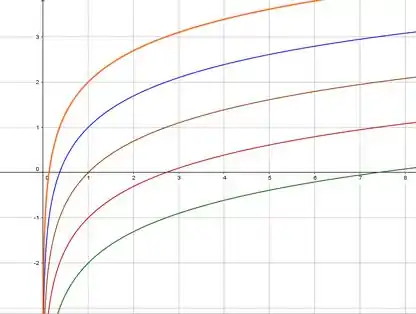
Faça o mapa de contorno da função mostrando várias curvas de nível.
Passo 1
Opa, fala ai belezinha? Vamos seguir com nossos estudos pra ficar fera na matéria!
Pra achar as equações das curvas de nível, a gente precisa igualar a função a uma constante qualquer :
Ou seja, só precisamos esboçar vários gráficos dessa forma, fazendo variar o .
Passo 2
Quando acrescentamos uma constante numa função, deslocamos seu gráfico na vertical. Dá uma olhada:
Vou usar o exemplo de uma função um pouco mais conhecida, que é , que vou desenhar em verde e em laranja, para mostrar como é esse deslocamento
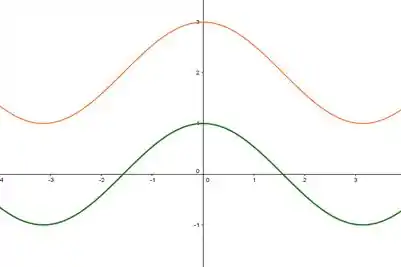
E basicamente nessa questão vamos ter que fazer a mesma coisa, mas com a função , deslocando o gráfico pra cima e pra baixo!
Passo 3
O gráfico da função é assim, lembra?
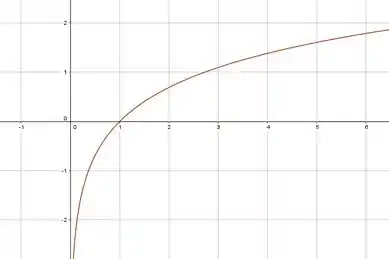
Agora é só deslocar o gráfico várias vezes! Ele não disse quantas exatamente, mas fazendo umas ou deve ficar de bom tamanho.
Passo 4
Fazendo valer e , o que resultou nesse lindo arco-íris de curvas de nível, então a gente vai desenhar o mesmo gráfico só que deslocando ele pra cima, quando for positivo e pra baixo quando for negativo 😊
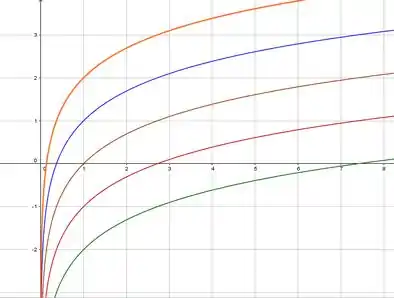
Resposta
