Em Pesquisa Operacional ou em Administração de Empresas é comum os cuidados com a otimização de processos, assim verifica-se que a função lucro da empresa ACÚSTIC é dada por dólares, onde x é o número de sistemas de som modelo F produzidos. Encontre onde a função é crescente e onde é decrescente.
Passo 1
O que o enunciado quer saber é, onde a função é crescente e onde é decrescente. Para isso precisamos lembrar da interpretação gráfica da derivada. A derivada é igual a inclinação da reta tangente ao gráfico. Vejamos um gráfico de uma função qualquer:
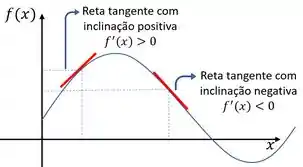
Repare que quando o gráfico da função é crescente (a curva está subindo), temos uma derivada positiva, e quando o gráfico da função é decrescente (a curva está descendo) a derivada é negativa. Então vamos usar essa informação aí pra matar essa questão.
Nossa função será:
CRESCENTE se
DECRESCENTE se
Então o primeiro passo é fazer a derivada de :
Observe o
Calculamos fazendo a derivada de cada termo:
Passo 2
Agora vamos ver em quais intervalos nossa derivada será positiva fazendo:
Bem, isso ai é uma inequação (porque tem aquele sinal de ali). Para resolver essa inequação, é bem parecido com resolver uma equação normal, vamos deixar o sozinho. Para isso vamos jogar o 300 que tá somando, para o outro lado subtraindo.
Agora tem um detalhe importante, o valor que acompanha o está negativo, para arrumar isso nós multiplicamos a inequação inteira por , e isso vai fazer com que todos os sinais se alterem, incluindo o sinal de (maior) que vai passar a ser (menor). Vai ficar assim ó:
Agora que o valor do já é positivo, vamos deixa-lo sozinho, passando esse 0,04 que está multiplicando, para o outro lado dividindo:
Isso significa que nossa função será crescente para todos os valores de que forem menores que 7500.
Passo 3
Agora vamos descobrir os valores onde a função será decrescente, lembrando que agora a derivada precisar ser negativa, ou seja, menor que zero.
Vamos deixar o sozinho aqui também:
E não se esqueça de multiplicar aqui por aqui também:
O que significa que nossa função será decrescente para valores de maiores que 7500.
A gente também pode confirmar isso olhando para o gráfico de :

Mas nem sempre temos o gráfico fácil a nossa mão, então a derivada ajuda a gente nessa tarefa aí.
Resposta
é crescente para
é decrescente para