Se qual é a única resposta correta para a sua primeira derivada?
Passo 1
Fala! Empolgada(o) para fazer exercícios de derivada? Fica tranquilo, porque aqui você vai entender tudo com um passo a passo bem explicadinho!
O primeiro passo é entender o enunciado! O que ele quer saber quando pergunta qual é a única resposta correta para a derivada da função abaixo?
Essa é só uma forma diferente de te pedir para derivar! O enunciado quis dizer: qual é a derivada desse em relação a ?
Representamos a derivada de em relação a como .
Como , achamos:
E por que ele pediu a primeira derivada? O que isso quer dizer? Existe a segunda derivada?
Quando ele pede a primeira derivada de , ele pede que você derive apenas uma vez! Se você derivasse duas vezes seguidas, você encontraria a segunda derivada de . Essa segunda derivada é representada da forma abaixo.
O número indica que essa é a derivada!
Mas não vamos perder o foco! Temos que resolver esse exercício e até agora só entendemos o enunciado! Então vamos fazer isso no próximo passo.
Passo 2
Para entender como derivar uma função com termos somados ou subtraídos, como é o caso da função , temos primeiro que lembrar como derivar cada termo separadamente!
Então, vamos olhar pra cada item da função, a começar pelo . Vamos nos lembrar como se deriva a constante presente em !
Derivar é a mesma coisa que calcular a taxa de variação! Então para que exista uma derivada é preciso que a função esteja variando. Mas se o termo não varia, como é o caso de uma constante, então sua taxa de variação vale zero!
Ou seja, como não varia em relação a , sua derivada vale .
Agora vamos olhar o termo presente em lá do início da questão? Como calculamos ele?
Passo 3
Calculamos a derivada de , usando a regra do peteleco! Essa regra é usada para derivar variáveis (como a variável ) que estão elevadas a uma constante! No nosso caso, temos que lembrar que a variável está elevada a !
Isso quer dizer que esse termo está elevado a uma constante. Logo, podemos usar a tal regra do peteleco!
Essa regra diz que, quando derivamos um termo elevado a uma constante , o expoente do termo “cai pra frente da função” e passa a multiplicar. Além disso, quando ele “cai pra frente da função, ele perde uma unidade”, ou seja, passa a ter um novo expoente !

No nosso caso, o expoente vale . Ao perder essa unidade, ficará no novo expoente. Assim:
Mas todo número elevado a zero é igual a . Então:
Pronto! Achamos a derivada de cada termo! Mas quanto vale a derivada de completo?
Veremos isso no próximo passo!
Passo 4
Nos passos anteriores vimos quanto vale a derivada de e a derivada de . Porém, ainda não vimos quanto vale a derivada total de !
Para calcular a derivada total, precisamos adaptar a regra de derivada da soma! Vimos que a derivada da soma é igual à soma das derivadas! Agora veremos que:
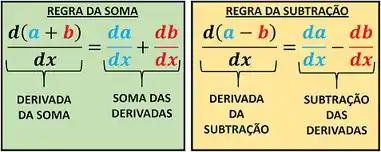
Ou seja, a derivada da subtração é a subtração das derivadas!
Aplicando isso em , encontramos sua derivada .
Nos já calculamos e ! Substituindo o que encontramos:
Resumindo, vale:
Aeeeee! Terminamos o exercício de derivadas! Esse passo a passo ajudou? Responde aí!