A área marcada B é três vezes a área marcada A. Expresse b em termos de a.
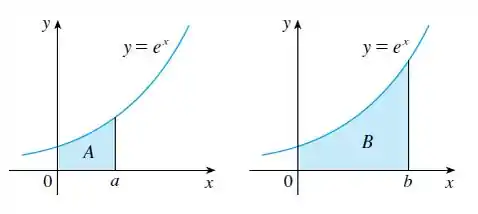
Passo 1
Bom, aqui nós queremos achar em termos de . Mas antes vamos lembrar que o problema nos disse:
(a área de é 3x a área de ).
Se lembram como calcular a área abaixo de um gráfico?
Usando a integral, não é? Então podemos escrever:
Integrando o , ficamos com:
Aplicando os limites:
Aplicando a distributiva:
Queremos isolar o para escrevê-lo em termos de , certo? Pra isso precisamos que ele saia desse exponencial. Como que a gente faz isso?
Aplicando o em ambos os lados! Até porque o é a inversa do exponencial
Como são inversos o e o exponencial se cancelam. Assim ficamos só com do lado esquerdo da equação.
Então:
E prontinho. Tá aí escrito em função de .