Calcule o limite:
Passo 1
Vamos ver mais essa aqui!
Substituindo diretamente o limite, nós caímos em uma indeterminação:
Não dá pra a gente fazer assim então. Vamos ver pelo meio da fatoração!
Passo 2
Para essa fração, o maior grau de cima é e de baixo é . Vamos coloca-los em evidência (dica: podemos fazer isso de um jeito bem direto, subtraindo cada expoente pelo grau do termo que estamos colocando em evidência). Veja
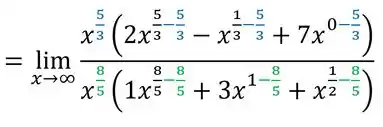
Vamos fazer agora aquelas subtrações ali nos expoentes com as frações...
Passo 3
A primeira subtração em cima é:
Depois
Aqui os denominadores são iguais, então a gente pode subtrair em cima e repetir o denominador:
A próxima que trava o nosso caminho é:
Aqui a gente pode escrever pra poder ficar com os mesmos denominadores
Agora falta:
Pra ficar com denominador igual, a gente pode multiplicar o por em cima e embaixo e o por :
Prontinho! Vamos jogar isso lá no limite agora!
Passo 4
Voltando aqui:
(Lembra que o negativo do expoente a gente pode eliminar jogando ele pra baixo)
Agora vamos simplificar esse que está na frente do parêntese em cima, com o na parte de baixo, também diminuindo os expoentes...
Passo 5
Olhando só para esses expoentes. Vamos fazer aqui:
Temos que deixar com denominadores iguais, então a gente pode multiplicar por em cima e embaixo, e por :
Reescrevendo lá então...
Passo 6
Vamos separar essa multiplicação assim agora:
Olha esse primeiro:
Passo 7
Beleza, o primeiro deu infinito, e o segundo?
Todos os termos com no denominador, com vão pra zero, lembra? Então aqui vai ficar:
Então...
Passo 8
Nosso limite é:
E finalmente, limite calculado! 😊