Calcule o limite ou prove que não existe:
Passo 1
Opa! Tudo bem?
Ao aplicarmos o limites nessa função vamos ter:
O que é uma indeterminação, então vamos procurar outro jeito pra resolver essa questão.
E aqui vai uma informação muito importante. Olha só: limites com divisão de polinômios indo a a gente pode sempre resolver do mesmo jeito, nós colocamos o termo de maior grau em evidência em cada polinômio. No nosso caso, o termo de maior grau é o .
Vamos colocar ele em evidência multiplicando e dividindo cada termo por . Tanto no polinômio que tá em cima, quanto no que tá embaixo.
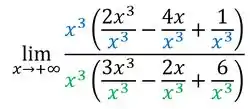
Agora a gente simplificar as frações que ficaram dentro dos parêntes:
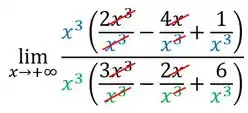
Como isso, ficaremos com:
(Lembrando que quando dividimos potências de bases iguais, repetimos a base e subtraímos os expoentes, por isso: por exemplo)
Passo 2
Agora podemos cortar o em cima e embaixo:
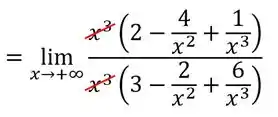
Ficando com:
Já melhorou bastante assim, agora podemos aplicar o limite novamente e ver se conseguimos um resultado que não caia em indeterminação novamente.
Todos os termos com no denominador zeram quando , lembra? Quando dividimos um valor por algo muito, muito muuuuuuuito grande o resultado será muito pequeno, indo a zero. Então aplicando o limite vai ficar:
E prontinho! Limite calculado! Viu como aquela dica de colocar o termo de maior grau dos polinômios em evidência salvou a gente? Então, guarda ela pra usar sempre que precisar! 😊