Encontre o limite
Passo 1
Olá! Tudo joia? Vamos ver mais esse limite que tem o indo pro infinito? Bora!
Olha só, se a gente tentar substituir aqui, vamos ter:
Isso aqui é tipo de indeterminação! Então a gente não pode ir por esse caminho...
E agora?
Calma, vem comigo!
Passo 2
Vamos fazer uma modificaçãozinha aqui...
Lembra que , então a gente pode reescrever o limite como:
Como nós temos em todos os termos, vamos colocar o em evidência. Pra isso, colocamos o multiplicando “do lado de fora”, abrimos os parênteses e dividimos todos os termos por . Assim:
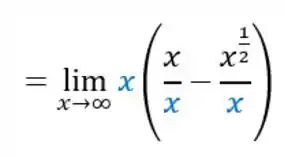
Passo 3
Na parte de dentro dos parênteses nós temos agora duas divisões, o que é igual a , e o onde a gente vai precisar usar uma propriedade de potenciação que diz que: na divisão de potências de bases iguais, a gente repete a base e subtrai os expoentes!
Vamos fazer isso separado aqui pra gente ver melhor como fica.
Lembrando que quando não tem nada do expoente a gente acrescenta o 1:
Temos essa continha no expoente pra resolver, então vamos escrever o como sendo pra que ele fique com o mesmo denominador que o :
Agora a gente resolve em cima e repete em baixo, ficando com:
Show, está quase bom. Pra ficar ainda melhor vamos ajeitar esse expoente aí que está negativo, jogando ele pra baixo pra ficar positivo. Assim ó:
E escrever ele em forma de raiz:
Beleza! Vamos encaixar isso no nosso limite agora😉
Passo 4
Nosso limite era assim:
E então fica assim:
Como agora tem uma multiplicação de por , a gente pode separar esse limite assim:
Vamos prestar atenção nesse pedacinho aqui:
Veja que a medida que aumenta, a raiz também aumenta, olha só:
Consequentemente, a divisão vai diminuir, pois vamos dividir o por um número cada vez maior...
Com isso, esse pedacinho: tende a zero, quando tende a infinito.
Passo 5
Entendendo isso, podemos aplicar agora podemos aplicar o limite na nossa função, e chegamos no seguinte:
E esse é o resultado do nosso limite!