Determine o limite abaixo

Pra começar vamos separar esse limite em duas partes, já que temos uma soma de duas frações ali:

E vamos resolver esse aqui primeiro:

Temos aqui uma divisão de dois polinômios. Agora presta atenção no grau desses polinômios: o termo que tem maior grau em cima é o , e embaixo é o . Então, a gente vai colocar eles em evidência multiplicando na frente, abrimos os parentes e dividimos cada termo do polinômio pelo termo de maior grau que a gente acabou de colocar em evidência. Vem comigo que vou lhe mostrar!

Vamos colocar o em evidência em cima e o em evidência na parte de baixo:

Não esquece de dividir cada termo que vai ficar dentro dos parênteses pelo que foi pra evidência, assim ó:

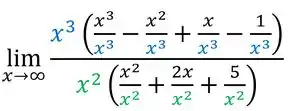
Podemos simplificar as frações que estão dentro dos parêntese:

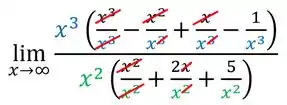
Simplificamos essas frações, diminuindo os expoentes, e vamos ficar com:

A gente pode ainda, simplificar o como o que estão na frente dos parênteses, diminuindo os expoentes pra ficar com:

Agora a gente pode separar isso em um produto:

Essa primeira parte dá infinito, certo?

E a segunda?

Bom, lembra que toda constante dividida por uma potência de , com dá zero?

Ou seja:

Olhando pro nosso limite então, todos aqueles termos com no denominador vão pra zero. Ou seja:

Juntando esse dois limites, temos:

Beleza! Vamos para aquele outro limite que estava somando lá no início, o:

Vamos fazer do mesmo jeito que o outro, só que aqui a gente vai colocar o em evidência em cima e embaixo, por ser o termo de maior grau...

Simplificando:

E podemos cortar o porque ele tá multiplicando em cima e embaixo, assim ficaremos com:

E como a gente já viu, todos os termos com no denominador vão pra zero, então...

Show, já temos o resultados dos dois limites.

O que ele pediu no enunciado foi o limite dessa soma:

E agora juntando o resultado dos limites, temos:

E acabamos por aqui! 😉