Calcule o sendo e
Passo 1
Para que seja possível realizar uma multiplicação entre matrizes, temos que ter o número de colunas da primeira matriz igual ao número de linhas da segunda matriz, ou seja:
Nesse caso, podemos ver que a matriz tem 2 linhas e 1 coluna, enquanto a matriz B tem 1 coluna e 2 linhas. Logo o resultado da multiplicação entre essas duas matrizes será uma nova matriz de dimensões .
Passo 2
Então, vamos multiplicar essas matrizes:
Olhando elemento por elemento, vemos que:
O está na primeira linha e na primeira coluna da matriz resultante. Então, para encontrar o valor de , precisamos multiplicar a primeira linha de com a primeira coluna de :

Logo:
Já o está na primeira linha, mas na segunda coluna. Então, para encontrar o valor de ,precisamos multiplicar a primeira linha de com a segunda coluna de :
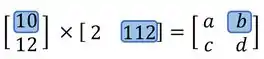
Logo:
Agora vamos olhar para o , que está na segunda linha e primeira coluna da matriz resultante. Assim, para encontrar o valor de ,precisamos multiplicar a segunda linha de com a primeira coluna de :

Logo:
Por fim, vemos que o está na segunda linha e na segunda coluna da matriz resultante. Logo, para encontrar o valor de ,precisamos multiplicar a segunda linha de com a segunda coluna de :
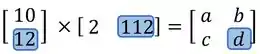
Logo:
Perceba que é a posição de cada elemento quem determina quais as linhas e colunas que serão multiplicadas.
Com isso chegamos então na resposta final! E encontramos nossa resposta.