Passe o sistema linear:
Para a forma matricial.
Passo 1
Bom pessoal, vamos pra mais um exercício. Você está vendo esse conjunto com as equações? São três equações:
Cada uma das equações tem três incógnitas , mas não estamos interessadas nas incógnitas, e sim, nos coeficientes que as acompanham, por isso vamos colocar todos os coeficientes junto das incógnitas. Lembrando que quando ela estiver sozinha, significa que seu coeficiente é igual a 1.
Então:
Passo 2
Nossa matriz será montada olhando a organização das equações:
São equações, então teremos linhas. E são incógnitas, mais um termo independente que está do lado direito do sinal de =. Então termos colunas.
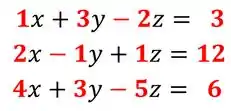
São os valores dos coeficientes de cada incógnita que vamos colocar na nossa matriz. E vamos organizá-los na ordem que vieram, ou seja, os valores dos coeficientes da primeira equação serão colocados na primeira linha, os da segunda equação na segunda linha e assim por diante.
Outro detalhe importante é que cada coluna vai corresponder aos coeficientes de uma determinada incógnita. Sendo assim, na primeira coluna, temos os coeficientes de , na segunda de , na terceira de , e na quarta estão os valores que ficaram do lado direito das igualdades.
Perceba uma coisa, o sinal de positivo e negativo de cada coeficiente é considerado na matriz.
Pronto, observado a organização das equações, chegamos na resposta final!