Dado que a matriz é dada pelos coeficientes numéricos do seguinte sistema linear:
E que seja igual a 2A. Defina os elementos que faltam da matriz
Passo 1
Vamos começar colocando o sistema linear na sua forma matricial, ok? O sistema é:
Vamos destacar quem devemos colocar na matriz:
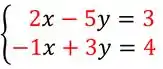
Lembrando que vamos colocar os coeficientes da primeira equação na primeira linha da matriz e os coeficientes da segunda equação na segunda linha:
Passo 2
Agora que já sabemos quem é a matriz , vamos multiplicar ela por 2 para descobrir quem é a matriz :
Beleza, nesse caso de multiplicação de uma matriz por um número real, devemos multiplicar todos os elementos dessa matriz pelo mesmo 2, dessa forma:
Vamos fazer essas multiplicações separadamente, ok?
Passo 3
Colocando os resultados em seus lugares:
Conseguimos então chegar aos resultados que faltam:
Ótimo, pessoal!
Resposta
Os resultados restantes são: -2, 6 e 6