Se A é uma matriz 2x3 e B é uma matriz 3x4, então o produto dessas matrizes terá qual dimensão?
Passo 1
Bom, na multiplicação de matrizes, precisamos sempre prestar atenção em um critério: o número de colunas da primeira matriz deve ser igual ao número de linhas da segunda. Ou seja, se temos:
Sendo uma matriz com colunas, a matriz tem que ter linhas para que a multiplicação seja possível.
Passo 2
Mas qual é o motivo pra isso? Vamos fazer um exemplo de multiplicação de matrizes pra isso ficar bem claro. Imagina uma matriz A:
é uma matriz 1x2, ou seja, a matriz te 1 linha e 2 colunas. Por outro lado, temos a matriz
Enquanto a matriz é uma matriz 2x3, pois tem 2 linhas e 3 colunas.
A multiplicação entre elas é possível:
Pois, temos o número de colunas da matriz é igual ao número de linhas da matriz :

E podemos prever que a matriz resultante dessa multiplicação, terá o mesmo número de linhas que a primeira matriz e o mesmo número de colunas da segunda matriz, nesse caso, a matriz resultante da multiplicação entre e , terá 1 linha ( tem 1 linha) e colunas ( tem 3 colunas).
Passo 3
O resultado da multiplicação de matrizes será uma nova matriz que tem seus elementos formados pela seguinte regra:
Para encontrar o valor de , faremos a soma dos produtos entre os elementos da primeira linha da matriz com a primeira coluna da matriz , veja:
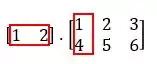
Logo:
Agora vamos encontrar o elemento . Para isso faremos a soma dos produtos entre os elementos da primeira linha da matriz com a segunda coluna da matriz , veja:
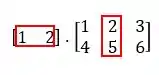
Logo:
E por último, para encontrar , faremos a soma dos produtos entre os elementos da primeira linha da matriz com a terceira coluna da matriz , veja:
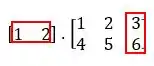
Logo:
Formando assim a matriz resultante.
Passo 4
Vimos com o nosso exemplo, que o que determina as dimensões da matriz resultante da multiplicação entre duas outras matrizes é o número de linhas da primeira matriz e o número de colunas da segunda:
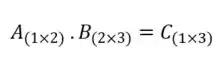
Entendeu direitinho? Agora vamos voltar para o enunciado!
Passo 5
No enunciado, falamos que temos a matriz de dimensões 2X3, enquanto a matriz tem as dimensões 3X4, logo temos:
Então essas matrizes podem ser multiplicadas e as dimensões da matriz resultante serão: