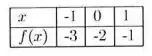
1. Dada a tabela de pontos abaixo, determine o polinômio interpolador usando os métodos de (a) Newton e (b) Lagrange. Os polinômios encontrados foram diferentes? Justifique sua resposta.
Passo 1
Falaaaa, rapaziada, beleza? Mais uma provinha de cálculo numérico! Hoje vamos rever um assunto muuuuito importante, a interpolação polinomial!
Podemos usar diferentes métodos para fazer uma interpolação, mas todos eles partem de um conjunto de pontos. Além disso, para pontos, encontramos um polinômio de grau menor ou igual a . Você pode até pensar: Mas por que? E aí é só lembrar da reta! Precisamos de apenas dois pontos para definir sua equação, que nada mais é do que um polinômio de primeiro grau ;)
Neste exercício temos 3 pontos tabelados, e , onde e . Logo, o polinômio interpolador terá grau menor ou igual à 2, ou seja, .
Vamos começar pelo método de Newton, beleza?
Passo 2
No método de Newton, o polinômio terá a seguinte forma: . Para determinarmos as constantes e , devemos resolver o seguinte sistema linear:
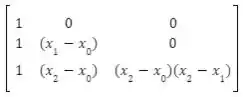
Substituindo as variáveis, obtemos o seguinte sistema:

Logo, e Substituindo na equação de , obtemos:
E é isso, galera! Suave, né? Vamos então para o método de Lagrange?
Passo 3
Bem galera, o polinômio também segue uma equação no método de Lagrange,, em que:
e
Substituindo na equação de , obtemos:
E essa foi justamente a resposta obtida pelo método de Newton! Isso acontece pois todos os pontos tabelados são diferentes, e como os métodos são baseados em resolução de sistemas, a solução é única.

Resposta
Os polinômios encontrados foram iguais, pois a tabela apresenta um conjunto de pontos distintos, isto é, a solução dos métodos é única.