O acionamento do cilindro hidráulico provoca o alongamento de na taxa constante de . Calcule a aceleração normal do ponto em sua trajetória circular em torno de para o instante em que .
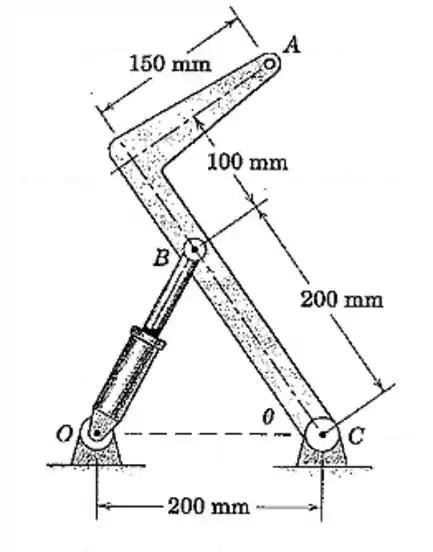
Passo 1
Nesses tipos de questões temos que achar uma relação trigonométrica entre o que queremos saber e o que temos de informação. A informação que temos é que a velocidade de é de . Então, vamos achar alguma relação trigonométrica com o comprimento :
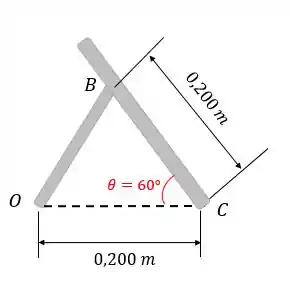
Repare neste triângulo formado. Podemos escrever o comprimento como:
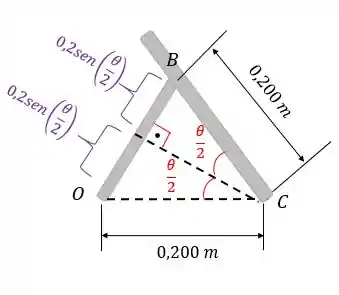
Passo 2
Derivando a equação que achamos vamos obter a equação da velocidade:
Para resolver esta derivada temos que usar a regra da cadeia, pois o ângulo varia no tempo:
Como e a velocidade de é , então:
Essa é a velocidade angular com que gira em torno de .
Passo 3
Agora vamos ver o que está acontecendo com o ponto :
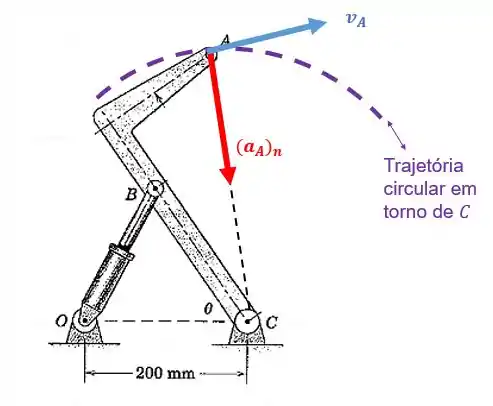
A questão pede a aceleração normal que é calculada pela seguinte fórmula:
Para achar o raio, vamos usar o seguinte triângulo:
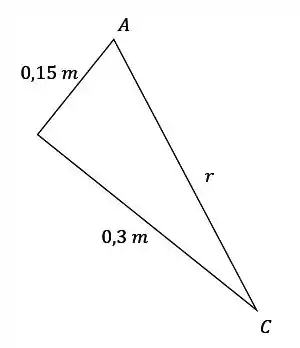
Como é um triângulo retângulo, vamos aplicar o Teorema de Pitágoras:
Agora sim podemos calcular a aceleração normal do ponto :