O cursor se desloca na ranhura horizontal com uma velocidade constante por um curto intervalo de movimento. Determine a velocidade angular da barra em termos do deslocamento .
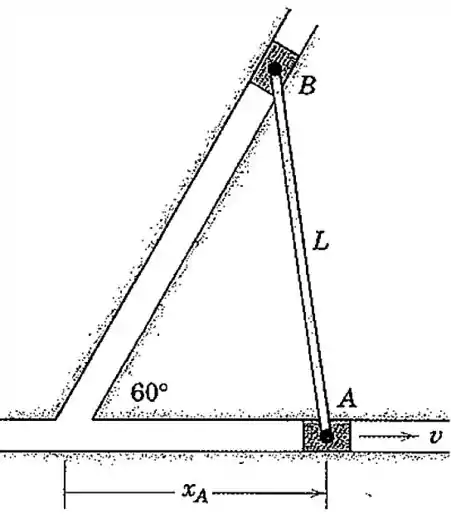
Passo 1
Nosso primeiro passo neste tipo de questão é achar uma relação trigonométrica que relacione a posição com a posição angular da barra .
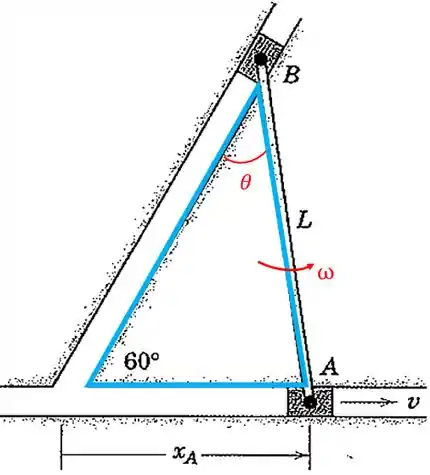
Repare que temos um triângulo formado dentro da figura:
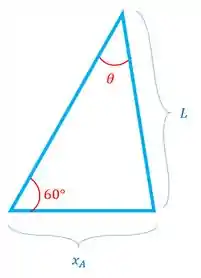
Vamos usar a lei dos senos para relacionar essas coisas:
Então a posição será:
Passo 2
Agora vamos achar a velocidade da barra . Para isso, é só derivarmos a equação da posição que acabamos de achar:
Repare que deixei tudo que é constante fora da derivada. Então, como o ângulo varia no tempo temos que aplicar a regra da cadeia:
Sabendo que
Então, teremos:
A barra está se movendo com uma velocidade constante e que foi chamada de , então:
A nossa equação da velocidade vai ficar:
Mas essa velocidade é dada no enunciado. O que queremos saber é a velocidade angular da barra . Então, vamos isolar na nossa equação:
Beleza?
Passo 3
Maaaas.... O enunciado pede a velocidade angular da barra em função de , ou seja, temos que arranjar um jeito de sumir com o ângulo e fazer surgir .
Lembra da lei dos senos que usamos lá no início do exercício? Vamos pegar aquela equação de volta:
Só que agora vamos isolar o e deixar tudo em função de :
Agora é só substituir isso na nossa equação da velocidade angular? Bem que poderia, mas lá não tem :
Tem apenas !!! Então, vamos pensar em uma relação trigonométrica que relacione seno e cosseno...
Agora sim!!! Vamos isolar o nessa relação aí:
Mas sabemos que o nosso é:
Então, vamos substituir esse valor de na nossa relação que acabamos de montar:
Vamos ter que:
Agora sim podemos substituir o na equação da velocidade angular:
Então, nossa equação da velocidade angular da barra é: