A barra gira uniformemente em torno do eixo em com velocidade angular constante . Determine a velocidade e a aceleração da barra que é obrigada pelas guias a se mover verticalmente.
Passo 1
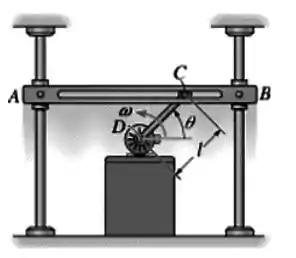
Primeiro vamos entender o que está acontecendo: a barra está girando em torno do ponto e conforme o ângulo aumenta a barra sobe.
A questão pede a velocidade e aceleração do movimento vertical da barra . Ou seja, temos que arranjar um jeito de relacionar o ângulo com a posição vertical da barra .
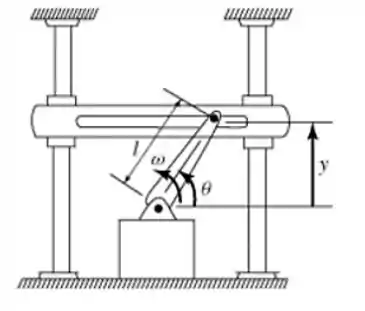
Repare que temos o seguinte triângulo retângulo:
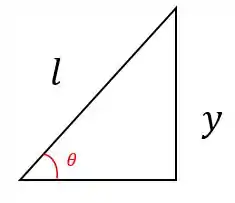
Para relacionar com o ângulo é só usarmos o seno:
Essa é a equação da posição da barra . Beleza?
Passo 2
Passo 3
Mas queremos saber a velocidade, não é mesmo? Então vamos derivar essa equação que achamos:
Como o comprimento da barra é constante, então:
Como o ângulo varia no tempo, para resolver esta derivada temos que aplicar a regra da cadeia:
Mas lembra que a velocidade angular é:
Então:
Passo 4
Agora falta a aceleração. Vamos derivar a equação da velocidade:
Vamos ter que aplicar a regra do produto e a regra da cadeia:
Temos que lembrar que:
E:
Vamos substituir na nossa equação:
Vamos dar uma ajeitada nisso:
Mas repare que no enunciado foi dito que a barra gira uniformemente em torno do ponto , ou seja, seu velocidade angular é constante. Portanto, a aceleração angular é zero:
Então, a nossa equação fica:
É isso aí!