O bloco de concreto está sendo abaixado pelo arranjo de cabo e polia mostrado. Se os pontos e têm velocidades de e , respectivamente, calcule a velocidade de , a velocidade do ponto para o instante representado, e a velocidade angular da polia.
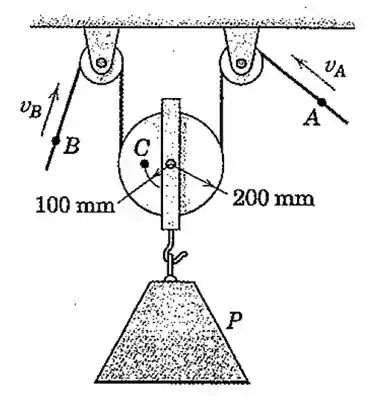
Passo 1
A velocidade do ponto é igual a velocidade onde o cabo do lado esquerdo encontra a polia central. E a mesma coisa ocorre no ponto onde o cabo do lado direito encontra a polia do meio. Então, vou chamar esses pontos também de e por terem a mesma velocidade:
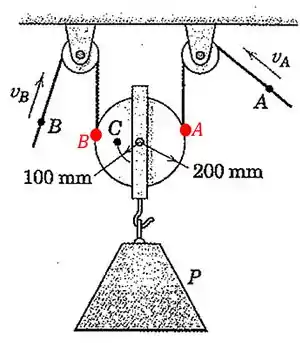
Vamos fazer uma linha ligando os pontos , e para ver o que está acontecendo:
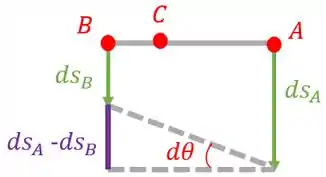
Repare que os vetores e apontam para baixo, porque o bloco está descendo. E como a velocidade do ponto é maior do que a velocidade do ponto , vamos ter que:
Passo 2
Agora vamos analisar como um movimento circular:
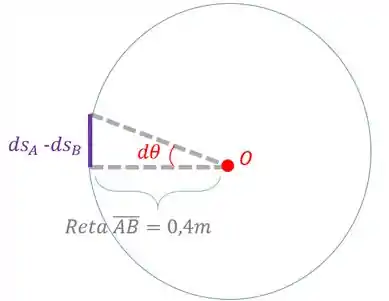
Vamos ter que a variação da posição entre os pontos e () será igual ao comprimento do arco do círculo que é a trajetória do movimento:
Agora é só derivar para achar a velocidade:
Sabendo que:
Então:
Vamos isolar a velocidade angular que é o que não sabemos:
Vamos substituir o que já sabemos: , e
Essa é a velocidade angular da polia.
Passo 3
Agora temos que achar a velocidade do bloco . Para isso, vamos fazer uma reta ligando os pontos e o centro da polia que vamos chamar de :
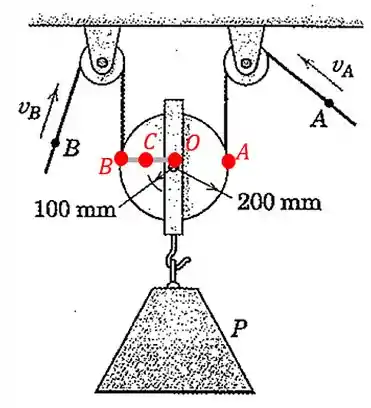
Teremos o seguinte:
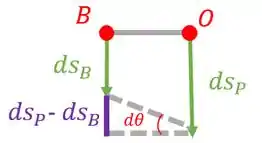
A nossa equação da posição vai ficar:
Para achar a velocidade é só derivar:
Como queremos a velocidade do bloquinho , então vamos isolar na equação:
Já sabemos que , e , então:
Passo 4
Agora falta acharmos a velocidade do ponto . Para isso, vamos fazer uma reta ligando os pontos e :
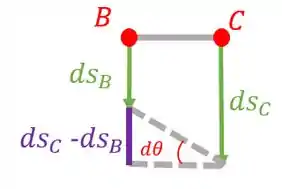
Temos que:
Para saber a velocidade do ponto é só derivar:
Vamos isolar que é o que queremos saber:
Repare que é:
Agora é só substituirmos os valores que já temos: ,
Essa é a velocidade do ponto .