No instante em que , a guia está subindo com aceleração de e velocidade de . Determine a aceleração e a velocidade angulares da barra no instante em considerado. Observação: o movimento para cima da guia ocorre no sentido negativo de .
Dado:
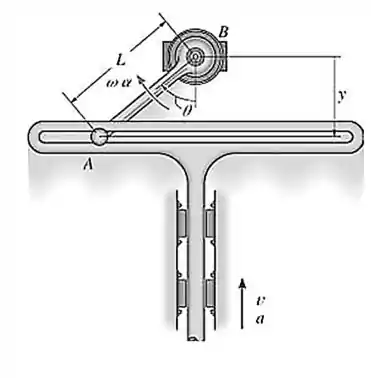
Passo 1
O que temos que fazer nesses tipos de questões é achar uma relação trigonométrica entre o que queremos saber e o que temos de informação.
Para começar vamos colocar em função das nossas informações:
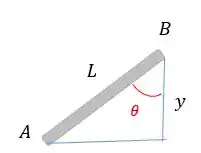
Podemos dizer que:
Derivando isso, vamos achar a equação da velocidade. Para derivar isso aí temos que usar a regra da cadeia:
Com essa equação podemos achar a velocidade angular da barra , pois sabemos que e .
Repare que o sentido positivo do eixo é apontando para baixo, certo? Então, a velocidade será negativa:
Agora vamos substituir tudo na nossa equação:
Passo 2
Derivando agora a equação da velocidade, vamos obter a equação da aceleração. Mas para derivar temos que usar a regra da cadeia e a regra do produto:
Com essa equação vamos achar a aceleração angular da barra .
Mas antes repare que a aceleração da guia está apontando no sentido negativo do eixo , então:
Substituindo o que temos: