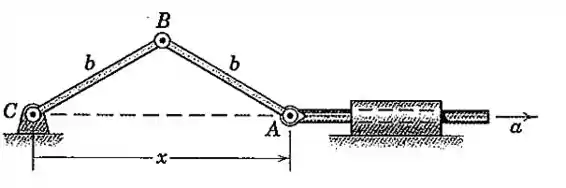
O ponto recebe uma aceleração constante para a direita a partir do repouso com essencialmente nulo. Determine a velocidade angular da barra em termos de e .
Passo 1
Nosso primeiro passo é arranjar um jeito de relacionar a posição da barra com o ângulo .
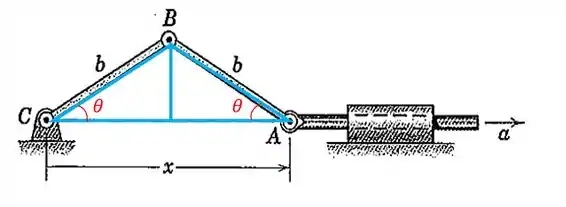
Para isso, repare nos dois triângulos retângulos que as barras formam:
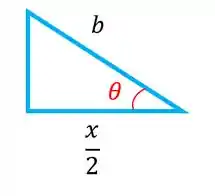
Usando trigonometria obtemos a seguinte relação:
Então:
Pronto, temos a equação da posição da barra .
Passo 2
Vamos derivar a equação da posição para obtermos a velocidade:
O comprimento das barras é constante e o ângulo depende do tempo, então vamos aplicar a regra da cadeia:
Não esqueça que a velocidade angular é:
Então, vamos ter:
A questão pede a velocidade angular da barra , então vamos isolar ela na equação:
Passo 3
Repare que a questão pede a velocidade angular da barra em função de e da aceleração . Veja que o enunciado disse que a aceleração é constante, então podemos usar uma daquelas equações de movimento retilíneo para aceleração constante.
Mas tem que ser uma equação que relacione a velocidade, a aceleração e a posição. Vamos usar essa aqui:
Sabemos que as barrinhas partem do repouso e que a velocidade inicial é nula, então:
Então:
Opa, agora vamos substituir isso na equação da velocidade angular :
Agora só falta retirarmos a variável da equação e fazer aparecer o . Nesta parte vamos ter aquela sacada de mestre. Sabemos da trigonometria que:
Isolando o vamos ter:
Vamos substituir isso na nossa equação:
Por que fizemos isso? Porque a equação que aparece o é a primeira que achamos:
E nessa equação também aparece o , por isso tínhamos que fazer aparecer o na nossa equação de velocidade angular.

Está quase terminando...
Vamos isolar o :
E agora substituir na equação da velocidade angular:
Pronto? Teoricamente sim, mas podemos deixar nossa equação mais bonitinha. Para isso, vamos passar o para dentro da raiz:
E é só alegria:
Esse sinal negativo indica que a velocidade angular está no sentido horário, então podemos escrever: