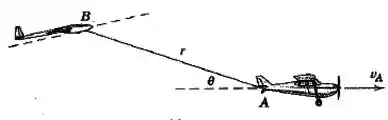
O avião está voando horizontalmente com uma velocidade constate de e está rebocando o planador , que está ganhando altitude. Se o cabo de reboque tem um comprimento e está aumentando na taxa constante de graus por segundo, determine os módulos da velocidade e da aceleração do planador para o instante em que .
Passo 1
Opa, vamos começar essa questão com uma reflexão: os dois aviões estão conectados por uma corda, certo?
O comprimento da corda se altera?
Não!
O que é relativo entre os dois aviões e se altera com o tempo?
O ângulo entre eles, que cresce a uma taxa de .
Passo 2
Sabemos que:
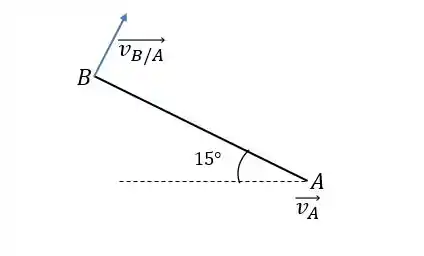
E como comentamos, a velocidade relativa entre e tem a ver com a variação angular. Podemos escrever:
Assim:
Passamos pra radianos, tá vendo?
Agora:
Passo 3
Bom, como o ângulo na horizontal vale , o ângulo entre e vale :
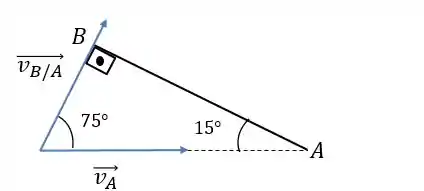
Assim, pra somarmos os vetores e vamos usar a regra do paralelogramo:
A velocidade em será:
Assim:
Passo 4
Só que:
Então:
E quem é Como está girando em torno de , essa vai ser a aceleração centrípeta:
Assim: