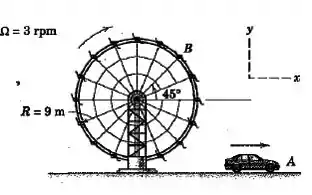
O carro tem uma velocidade para a frente de e está acelerando a . Determine a velocidade e a aceleração do carro em relação ao observador , que é levado em uma cadeira sem rotação sobre a roda-gigante. A velocidade angular da roda-gigante é constante.
Passo 1
Novamente, vamos usar:
Onde é a velocidade relativa entre os móveis.
Passo 2
Bom, a velocidade do carro é, em
Passo 3
A frequência de rotação está em . Para transformar para , basta dividir por
E a velocidade angular é:
Passo 4
A velocidade tem uma direção dada por:
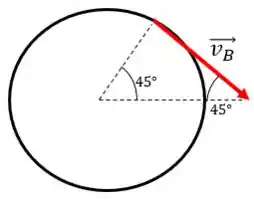
Quanto vale o módulo de ? Ele é dado por:
Assim:
Por que o sinal negativo em Porque a velocidade está com a componente vertical apontando para baixo.
Assim, podemos dizer que:
Passo 5
A única aceleração do móvel é a aceleração centrípeta:
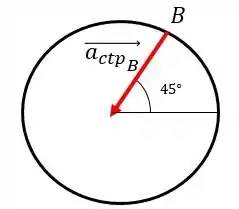
Seu módulo é dado por:
E:
E a aceleração de
É só:
Assim: