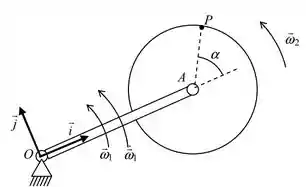
01) Em um dado instante, a haste , de comprimento , tem velocidade angular e aceleração angular Em sua extremidade está articulado um disco de raio , o qual gira com velocidade angular constante em relação à haste. Adotando a haste como referencial móvel, pede-se determinar:

a) o vetor rotação absoluta do disco;

b) o vetor aceleração rotacional absoluta do disco;

c) as velocidades relativa, de arrastamento e absoluta do ponto P do disco;

d) as acelerações relativa, de arrastamento, de Coriolis e absoluta do ponto do disco;

b) Agora devemos determinar o vetor aceleração rotacional absoluta do disco.

Esse vetor tem a mesma cara do anterior, de ser tipo um vetor aceleração angular resultante dos movimentos que o corpo realiza. Só que, tem uma diferençazinha, lembra qual é?

Hahaha. É que surge uma aceleração também devido aos diferentes movimentos de um mesmo corpo. Nesse caso, ela é dada por:

Então bora lá, o vetor aceleração rotacional absoluta será dado por:

Tem alguns detalhes importantes pra perceber aqui. Pelo enunciado, é constante, logo a derivada de é nula, isto é, . Daí:

E é isso!! Bora pro próximo 😉

c) Agora devemos calcular as velocidades relativa, de arrastamento e absoluta do ponto do disco.

Sabe o papo que comentamos agora há pouco sobre o movimento direto e indireto realizado pelo disco?! Então, o ponto passa pela mesma coisa.

A velocidade relativa que a questão nos pede é, basicamente, a velocidade em relação a um referencial no próprio disco, sacou?

Nesse caso, é uma dica legal usar o centro do disco, pois ele está parado nesse referencial. Assim:

Viu? . Isso já ajuda bastante. Além disso, pela figura também podemos dizer que:

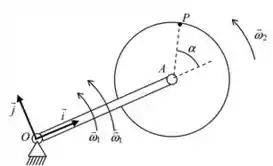
Substituindo, temos:

Logo:

Bouaa!

Vamos pensar agora na velocidade de arrastamento.

Aqui temos que pensar no movimento “indireto” que falamos anteriormente. Como a barra está girando, indiretamente o ponto também irá girar. Esse é o movimento de arrastamento.

Pra calcular estamos interessados apenas na velocidade dada ao disco por esse movimento, entendeu? Então, podemos usar o ponto , que está parado. Assim:

Daí, como o ponto está parado, temos . Além disso:

Substituindo, temos:

Show!

Pra finalizar e encontrar é só considerar a resultante desses dois movimentos, ou seja, a soma dessas duas velocidades:

Foooi! É isso aí.

d) Pra finalizar essa questão, devemos determinar a aceleração relativa, de arrastamento, de Coriolis e absoluta do ponto .

Novamente, a ideia da aceleração relativa é usar o mesmo referencial no qual o disco está se movimentando, ou seja, considerando apenas o movimento direto. Beleza?

Daí, usando novamente o ponto como referencial, temos:

Lembrando que nesse referencial o ponto está parado, logo . Além disso, é constante, ou seja, . Portanto:

Logo:

Prontinho!

Pra aceleração de arrastamento vamos usar a mesma ideia do . Daí, podemos escrever:

Novamente, como é fixo temos . Além disso, como encontramos no item c):

Assim:

Só organizando um pouco mais, temos:

Show de bola!

A aceleração de coriolis está relacionada justamente ao novo movimento que surge da composição do “direto” e do “indireto”. Matematicamente, ela vale:

Como calculamos no item b) e c), temos:

Excelentee!!! Pra calcular a aceleração absoluta basta somar tudo:

+

Que expressão giganteee né?! Mas é isso mesmo, podemos organizar um pouquinho mais só:

Pronto galera, é isso aí! Finalizamos mais uma questão.

Curtiram? Agora é dar uma respirada, beber uma água e depois voltar no gás 😊