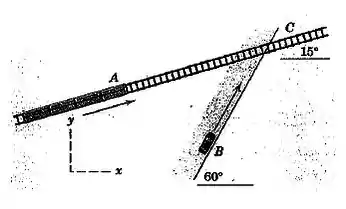
O trem viaja com uma velocidade constante ao longo da estrada de ferro reta e horizontal. O motorista do carro , antecipando a passagem de nível ferroviária , diminui a velocidade do carro de na taxa de . Determine a velocidade e a aceleração do trem em relação ao carro.
Passo 1
A velocidade do trem, , pode ser escrita como:
Assim, a velocidade relativa de em relação a é:
Passo 2
Podemos escrever o vetor usando o ângulo de
E o
Assim:
Passo 3
A aceleração relativa será calculada da mesma forma:
Sendo que a aceleração do trem é nula: .
E:
Por que negativo? Porque é uma desaceleração. Está agindo no sentido contrário ao movimento de
Assim:
Resposta
Exercícios de Livros Relacionados
O avião A está voando horizontalmente com uma velocidade constante de 200k m / h e está rebocando o planador B , que está ganhando altitude. Se o cabo de reboque tem um comprimento r = 60m e θ está au
O trem A viaja com uma velocidade constante v A = 120k m / h ao longo da estrada de ferro reta e horizontal. O motorista do carro B , antecipando a passagem de nível ferroviária C , diminui a velocida
O jato de transporte B está voando para o norte com uma velocidade v B = 600k m / h quando uma aeronave menor A passa por baixo do transporte dirigida na direção 60 ° mostrada. Para os passageiros em
A catapulta de lançamento do porta-aviões fornece ao avião de caça uma aceleração constante de 50m / s ² ² a partir do repouso em relação ao convés de vôo e lança a aeronave a uma distância de 100m me
Um rebatedor acerta a bola de beisebol A com uma velocidade inicial de v 0 = 30m / s diretamente para o jogador B com um ângulo de 30 ° com a horizontal; a posição inicial da bola é 0,9m acima do níve