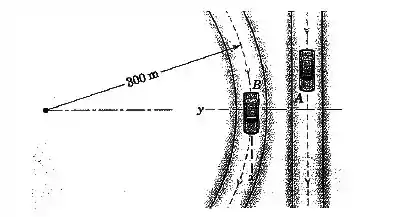
Para o instante representado, o carro tem uma velocidade de , que está aumentando na taxa de cada segundo. Simultaneamente, o carro também tem uma velocidade de enquanto contorna a curva e está reduzindo a velocidade na taxa de cada segundo. Determine a aceleração que o carro aparenta ter para um observador no carro .
Passo 1
Vamos primeiro analisar o carro
O enunciado diz que a velocidade do carro aumenta em a cada segundo. Essa é a aceleração:
Passo 2
Agora vamos analisar
O carro tem uma aceleração tangencial, já que a sua velocidade diminui, e uma centrípeta, já que faz uma curva:
A sua velocidade no instante considerado vale:
E a aceleração centrípeta:
Passo 3
Colocando todos os vetores em um mesmo plano:
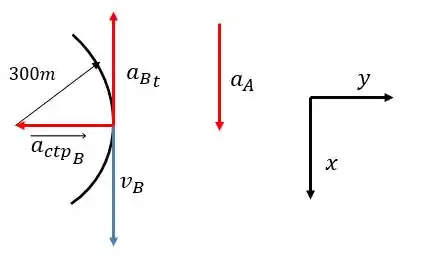
Escrevendo o vetor
O vetor
Assim, usando a nossa velha fórmula: