A posição de uma partícula é dada por , onde é em metros e é em segundos. Represente graficamente a posição, velocidade, e aceleração como funções do tempo para os primeiros segundos de movimento. Determine o instante em que a velocidade é zero.
Passo 1
Bom, como vimos, a derivada da posição pelo tempo é a velocidade:
E a aceleração é a derivada da velocidade, também pelo tempo (ou segunda derivada da posição):
Passo 2
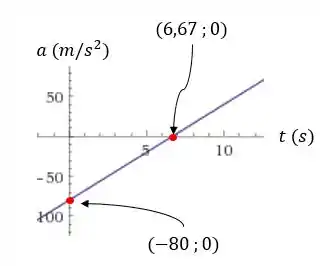
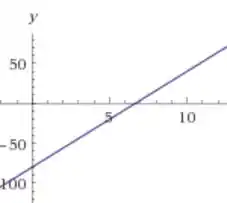
Galera, vamos construir os gráficos aqui. Acho legal começarmos pelo gráfico da aceleração, que é uma reta:
Sendo uma reta a gente precisa apenas de dois pontos para traçar o gráfico, vamos fazer então e . Dessa forma, a gente acha os seguintes pontos:
E
Então achamos os dois pontos :
Assim podemos traçar o gráfico:
Passo 3
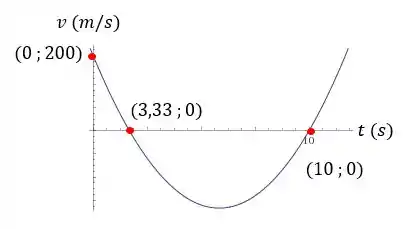
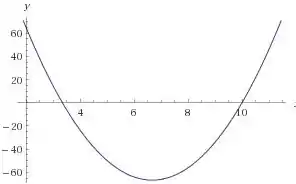
Agora vamos fazer o gráfico da velocidade, que é uma parábola:
Para uma parábola nós precisamos de três pontos para desenhar o gráfico. Sendo assim, vamos encontrar as duas raízes e o ponto onde a função corta o eixo .
Começando pelo ponto onde a função corta o eixo vamos ter:
Logo, temos o ponto . Agora partiu para as raízes:
Portanto, temos os pontos e . Então o gráfico da velocidade fica desta forma:
Passo 4
E podemos fazer o gráfico do deslocamento também. Pessoal, esse gráfico já um pouco mais chato e precisa de 4 pontos para ser produzido. Então vou colocar o gráfico aqui e vamos apenas fazer algumas análises:
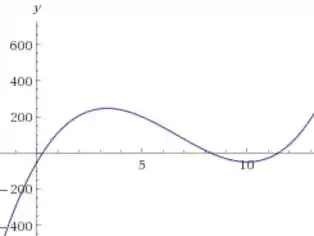
A primeira derivada (que é a velocidade) nos fornece os máximos e mínimos locais quando se iguala a zero. Dá pra ver pelo gráfico que são os mesmos valores de :
Além disso, temos também os pontos de inflexão que são dados pela segunda derivada (que é a aceleração), perceba que o ponto também tem o mesmo valor de :
Maneiro né!?
Passo 5
O instante em que a velocidade é nula nós já temos, que foi calculado no passo 3 e valem:
Resposta
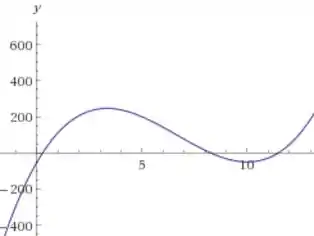
E: