Considere os orbitais atômicos e , admitindo respectivamente as funções angulares e . Determine, na ordem seguinte, o número total de superfícies nodais, a natureza das superfícies nodais derivando da parte angular e o número de esferas nodais destes dois orbitais.
Passo 1
A nomenclatura mundou um pouco, mas vamos entender que superfícies nodais são as nossas superfícies nodais angulares e esferas nodais são os nossos nodos radiais.
A gente sabe que o número total de nodos é dado por .
Então as duas funções de ondas acima, e , com , possuem 3 nodos.
E a gente também sabe que o número de superfícies nodais angulares é igual a .
Logo, as duas funções de ondas acima, e , com , possuem 3 superfícies nodais angulares, não tendo nenhuma esfera nodal.
Passo 2
Como é que a gente descobre a “natureza das superfícies nodais”?
Através da função angular do orbital a gente pode definir se as superífices são planas e quais equações descrevem essas superfícies.
Vamos ver como isso funciona.
Para a primeira função de onda, a função angular é:
O nodo é quando a função de onda é zero né? Então vamos igualar esse cara aí a zero:
E pra uma multiplicação ser igual a zero, um dos fatores é zero:
E o que que é esse ? Ele é a distância de um ponto qualquer em relação à origem. Olha aí:
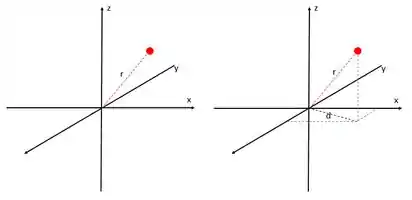
Aquela reta pontilhada em preto, que a gente chamou de d, é tipo a sombra da linha tracejada vermelha no “chão” (plano xy).
Por pitágoras, a gente vê que:
E então:
Aí a gente volta pra nossa função e substitui por , beleza?
O que que isso quer dizer?
Que a nossa função é igual a zero toda vez que:
é um plano, enquanto a outra superfície é bem mais complexa de enxergar. Normalmente teria que parametrizar e etc. Tem que ter uma base legal de cálculo. Mas são dois cones virados um contra o outro, assim:
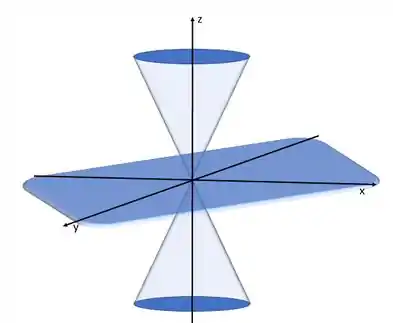
Vamos fazer a mesma coisa com a outra função:
Igualamos ela a zero e achamos:
Desenvolvendo a segunda equação:
Então a função é igual a zero sempre que ou .
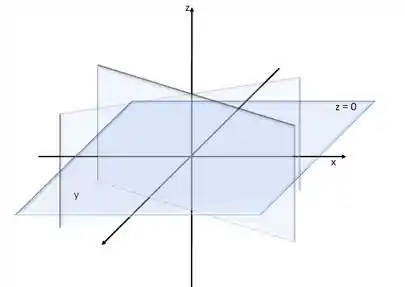
Resposta
Ei, a resposta está no passo a passo :)