1. A gente tem uma ideia de como essas superfícies limites são. Como o enunciado não explicita sobre quais eixos devemos desenhar, vamos fazer sobre qualquer um. É legal desenhar o 3d maior que o 2p, e o 2p maior que o 1s porque, como a gente comentou, o número quântico principal dá uma ideia do tamanho dos orbitais. Valeu?



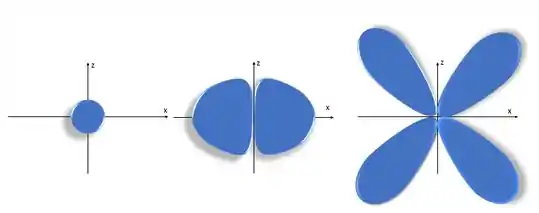
E aí estão os desenhos do 1s, 2p e 3d, respectivamente.

Passo 2

2. Nodo é o ponto onda a função de onda (orbital) muda de fase.

Isso basta!

Mas pra você entender um pouquinho melhor:

Lembra que o orbital nada mais é do que uma função matemática? Nem todas as funções matemáticas servem como função de onda. As funções de onda geralmente contém um “”, um “ ou outra função trigonométrica, que faça com que ela oscile, como uma onda.

Vamos olhar a função seno abaixo:



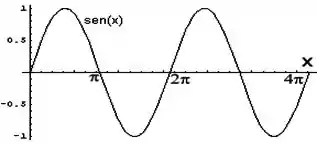
Cada vez que ela passa do positivo para o negativo ou do negativo para o positivo, dizemos que ela está mudando de fase.

A função seno acima muda de fase nos pontos e cada um desses pontos é chamado um nodo.

E lembra que a probabilidade de encontrar o elétron é igual ao quadrado dessa função?

Se a gente pegar a função aí de cima e elevar ao quadrado, todos os pontos negativos vão virar positivos (porque o quadrado de qualquer número é um número positivo).

Mas os pontos onde ela é zero, vão seguir sendo zero!

Pra um orbital, pra qualquer ponto onde a função de onda tiver valor zero, o quadrado dela também vai ser zero. E nesse ponto a probabilidade de encontrar o elétron é nula. Isso é o nodo!

Passo 3

3. Primeiro vamos definir o que é um nodo radial e o que é uma superfície nodal angular.

A gente já viu que no nodo, a probabilidade de encontrar o elétron é nula. Mas a probabilidade igual a zero não fica em um único ponto. O orbital tem três dimensões! A probabilidade zero de encontrar o elétron se estende por uma superfície!

No orbital p, por exemplo, toda a superfície entre as duas esferas achatadas tem probabilidade zero de encontrar o elétron. Então para x=0 (todo o plano delimitado pelo eixos z e y) temos uma superfície nodal.



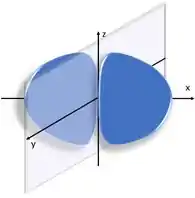
Agora, olhando para o orbital 2s, não existem planos nodais. No entanto, a gente calcula o número de nós (ou nodos) por . Como, para o 2s, , então temos um nó. Onde ele está? Lá dentro!

Em orbitais s, o nodo é definido por um determinado raio em relação ao núcleo. Ou seja, existe toda uma casca esférica delimitada por um certo raio de distância do núcleo onde a probabilidade de encontrar o elétron é nula.

Quando o nó é caracterizada por um raio fixo, chamamos de nodo radial.

Quando o nó não tem uma distância fixa do núcleo, existe um ângulo que é fixo (no nosso desenho é o ângulo do plano em relação ao eixo x, que é sempre de 90°) e temos uma superfície nodal angular (muitas vezes formando um plano).

Agora vamos falar de quantidade:

O número de superfícies nodais angulares é igual a . Ou seja: orbitais s não possuem superfícies nodais angulares, orbitais do tipo p possuem 1, e assim por diante.

Como o número de nós é igual a , o número de nós radiais vai ser dado pela diferença entre o número total de nós () e o número de nós angulares ().

Por exemplo:

3d: número de nós angulares: ; número total de nós: ; número de nós radiais: 0

5p: número de nós angulares: ; número total de nós: ; número de nós radiais: 3

4f: número de nós angulares: ; número total de nós: ; número de nós radiais: 0

Passo 4

4. Para o orbital 4f:

Como vimos, com , o orbital 4f possue 3 superfícies nodais angulares. Não necessariamente elas serão planas.

Vamos dar uma olhada nos orbitais do tipo f:

Com excessão do orbital f, todos os outros apresentam 3 planos nodais, tipo assim:

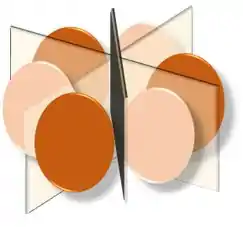
O orbital f apresenta 3 superfícies nodais angulares, mas apenas 1 é plana:

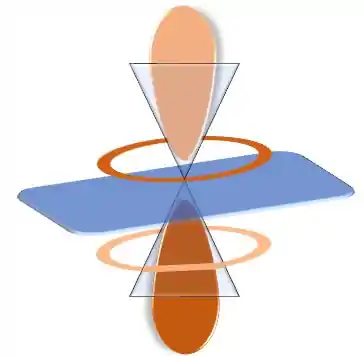
Onde os dois cones e o plano azul representam as três superfícies nodais angulares.