Considere duas fontes luminosas de ondas de mesmo comprimento de onda , mas que são geradas com uma diferença de fase igual a . As duas fontes estão separadas por uma distância .
Considere um observador que mede a intensidade da luz resultante, situado na linha reta que une as duas fontes, a uma distância de uma delas. Se este observador se mover ao longo do eixo ele verá:
Pontos de máximo e mínimo de intensidade quando variar .
Regiões de intensidade máxima para qualquer .
Regiões de intensidade mínima para qualquer .
Com os dados fornecidos não é possível afirmar nada.
Nenhuma das respostas anteriores.
Passo 1
Vamos imaginar o observador a uma distância de uma das fontes, na linha que liga ambas as fontes.
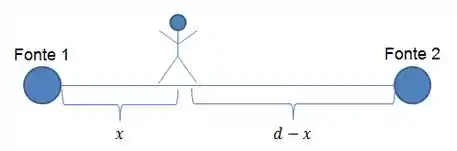
Antes de mais nada, a luz enviada pelas duas fontes já tem de cara uma diferença de fase de radianos. Vamos considerar que a diferença de fase é a fase da fonte 2 menos a da fonte 1.
Além dela temos uma diferença de fase devido à diferença entre os percursos percorridos pela luz da fonte 1 e da fonte 2.
Mas para ver essa diferença de fase, precisamos ver qual o valor de . Pela figura:
Para facilitar as contas (evitar números negativos), vamos considerar que esse valor seja sempre positivo, ou seja:
O motivo disso é que, na verdade, a diferença de percurso deveria ser o módulo da nossa subtração. Quando , a nossa subtração daria negativa, e seu módulo seria .
Substituindo tudo, a diferença de fase total fica:
Pelo enunciado, a distância é:
Assim:
Passo 2
Para que essa interferência seja construtiva, é necessário que:
Para isso, os valores de teriam que ser:
Se formos substituindo os valores de , notaremos que, até a metade do caminho, ele vê cinco pontos de máximo.
Eu substitui pra termos mais claro em que lugar da reta a pessoa irá ver aquele ponto de máximo.
Para ele enxergar uma interferência destrutiva:
Com isso:
Repetindo o raciocínio anterior, poderemos observar que ele verá quatro pontos de mínimo.
Ou seja, esses cálculos deixam claro que ele vai ver pontos de máximo e mínimo intercalados, com uma distância de entre um máximo e o mínimo que vem logo depois e o que vem logo antes.
Com isso, a resposta certa é a letra (a), pontos de máximo e mínimo de intensidade quando variar .
Resposta
Letra (a), pontos de máximo e mínimo de intensidade quando variar .