Duas antenas de rádio e irradiam em fase. A antena está a à direita da antena .
Considere um ponto ao longo da extensão da linha reta que une as duas antenas, situado a uma distância de à direita da antena .
A frequência e, portanto, o comprimento de onda das ondas emitidas pode variar.
- Qual é o maior comprimento de onda para o qual pode existir interferência destrutiva no ponto ?
- Qual é o maior comprimento de onda para o qual pode haver interferência construtiva no ponto ?
Passo 1
a)
Primeiro, devemos encontrar a diferença entre as distâncias das duas fontes até o ponto Q.
Vamos fazer uma figurinha pra ajudar a visualizar:
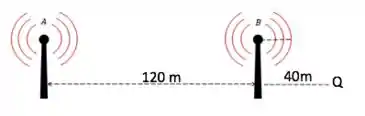
Para a fonte B, temos:
Para a fonte A, temos:
Logo,
Passo 2
Para que a interferência seja destrutiva, é necessário que:
Porém, invertendo a equação, temos:
Ou seja, é o maior possível para o menor possível, que é zero. Aplicando na equação, ficamos com:
Passo 3
Para que a interferência seja construtiva, é necessário que:
Quando temos , podemos inverter a equação e obter
Novamente, vemos que é o maior possível quando é o menor possível. Para , as duas fontes estariam no mesmo ponto, o que sabemos que não é verdade.
Assim, o menor possível é 1, que aplicando na nossa equação fica:
Resposta
a)
Para interferência destrutiva, temos que:
b)
Para interferência construtiva, temos que: