Dois alto-falantes emitindo ondas sonoras idênticas de comprimento de onda igual a em fase uma com a outra e um observador estão posicionados conforme a figura abaixo.
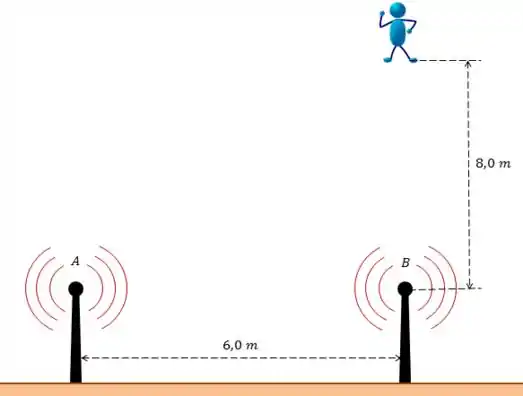
- No local onde está o observador, qual é a diferença entre os caminhos das ondas provenientes dos dois alto-falantes?
- As ondas sonoras irão interferir construtivamente ou destrutivamente no local onde está o observador?
Passo 1
a)
A distância do alto-falante ao observador pode ser achada imaginando-se um triângulo retângulo onde é a hipotenusa. Assim:
A distância do alto-falante ao observador é dada a partir da imagem, de modo que:
Logo:
Passo 2
b)
Dizemos que há interferência construtiva quando:
Da mesma maneira, dizemos que há interferência destrutiva quando:
O problema nos diz que . Logo, os pontos de interferência construtiva serão quando a diferença entre os caminhos for igual a:
Da mesma forma, os pontos de interferência destrutiva serão quando a diferença entre os caminhos for igual a:
Na letra a), vimos que . Logo, o ponto onde o observador está é um ponto de interferência construtiva.
Resposta
a)
b)
O ponto onde o observador está é um ponto de interferência construtiva.