Ondas longas de rádio, com comprimento de onda , de uma estação radioemissora podem chegar a um receptor por dois caminhos diferentes.
Um deles é uma trajetória retilínea do emissor até o receptor, a uma distância .
O segundo envolve uma reflexão na ionosfera (camada de moléculas de ar ionizadas, quase no topo da atmosfera) que está a uma altura da superfície da Terra.
Admita que a reflexão ocorra num ponto a meio caminho do emissor e do receptor e que a onda sofra uma mudança de fase de radianos ao ser refletida pela ionosfera.
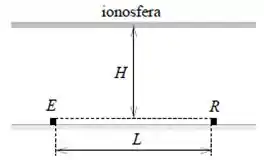
- Que condições devem ser obedecidas entre , e para que haja uma interferência destrutiva entre o feixe direto e o feixe refletido?
- A ionosfera começa a uma altura de aproximadamente . Se a frequência do emissor é igual a e a distância entre a estação e o receptor é igual a mostre que nenhum sinal é recebido pelo receptor.
Dado: Velocidade da luz
Passo 1
Letra a)
A diferença de fase por diferença de caminho é dada por:
Mas além dessa diferença de fase, temos uma diferença de fase por reflexão:
A diferença de fase total é a soma das duas:
Para que a interferência seja destrutiva:
Substituindo:
Precisamos então achar a diferença entre os dois caminhos.
Passo 2
Para achar a diferença entre os caminhos, temos um problema de geometria. O caminho da luz que não reflete na ionosfera é:
Para aquele que reflete, nós temos o caminho que ele faz até a ionosfera e depois o caminho que ele faz da ionosfera até o receptor. Esses dois caminhos tem igual magnitude e, para encontrá-los, podemos usar o teorema de Pitágoras no triângulo retângulo.
Então:
Logo, para termos interferência destrutiva:
Passo 3
Letra b)
Primeiro, encontremos o comprimento de onda deste sinal.
Substituindo:
Vamos testar a condição de interferência destrutiva:
Como essa equação resulta em um número inteiro, então temos uma interferência destrutiva.
Resposta
Letra a)
Letra b)