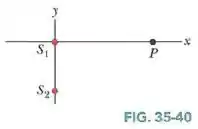
Na Fig. 35-40, duas fontes pontuais isotrópicas, e , estão sobre o eixo y, separadas por uma distância de , e emitem em fase com um comprimento de onda de .
Um detector de luz é colocado no ponto P, situado sobre o eixo x, a uma distância da origem.
Qual é o maior valor de para o qual a luz detectada é mínima devido a uma interferência destrutiva?
Passo 1
Vamos começar aos poucos, com o que sabemos.
Seja a distância entre e e a distância entre e . Para que a interferência em seja destrutiva, é necessário que:
Assim, a primeira coisa a fazer é encontrar .
Passo 2
Para , vemos que ele está no eixo x, assim como . Logo,
Para , podemos imaginar um triângulo retângulo formado por , e . Isso nos dá, pelo teorema de Pitágoras:
Agora sim, estamos em condição de escrever uma expressão para a diferença dos caminhos de e para .
Passo 3
Com a expressão para a diferença das distâncias, o resto da questão é manipular as expressões pra chegarmos no nosso objetivo. Sabemos que
Vamos passar para o lado direito, e elevar os dois lados ao quadrado.
Vamos expandir a expressão à direita, e dar 3 passos, para chegar numa expressão melhor para nós.
Essa expressão ainda está um pouco feia, mas vai nos ajudar num pequeno raciocínio.
Note que quando aumenta, o numerador diminui, diminuindo . Além disso, o denominador aumenta, também diminuindo . Isso significa que, a medida que aumentar, vai diminuir!
Então, para acharmos o maior tal que a interferência em é destrutiva, precisamos usar o menor possível, que é zero.
Passo 4
Com o que discutimos, vamos então substituir na nossa expressão.
Por fim, uma última mudança, pra equação ficar a melhor possível pra gente.
Mas o problema nos disse que . Com isso, finalmente, atingimos nossa resposta:
Resposta
O maior valor de possível para que a interferência seja destrutiva é .