Uma onda plana de comprimento de onda incide sobre a superfície de um cristal, mostrado em corte transversal na figura. Deduza a relação que deve haver entre , e para que os raios e mostrados na figura interfiram construtivamente (fórmula de Bragg-Williams).
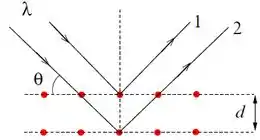
Passo 1
Antes de mais nada, não se assuste com nomes que possam ser estranhos no enunciado!
Vamos apenas fazer nossa missão com coragem: achar diferença de fase, e igualar a (interferência construtiva).
Primeiro, vamos entender o desenho. Um cristal é formado por várias moléculas (ou átomos) juntos de forma bem bonitinha, parece até soldados do exército em uma formatura. Olha só o sal de cozinha:
O raio reflete nos soldados (moléculas) da parte mais externa, enquanto que o raio acaba errando a mira e reflete na segunda camada de soldados (moléculas).
Se a reflexão causar diferença de fase, ela causa nos dois raios igualmente, e não afeta nada.
Então, só sobra diferença de fase causada pela diferença de caminho. Vamos achá-la soldado!
Passo 2
Agora é geometria.
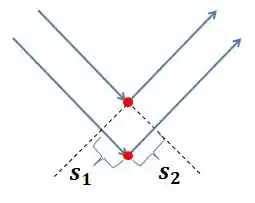
A não ser por e , a distância percorrida pelos raios é igual (nota que eles são paralelos e a partir das linhas tracejadas, saem “da mesma altura”).
Logo, a diferença de caminho vai ser e a diferença de fase em radianos fica:
Precisamos então deduzir quem é e quem é .
Passo 3
Para achar e , vou desenhar mais algumas coisas aqui:
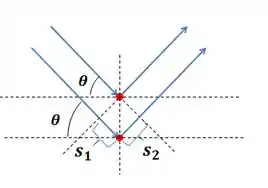
Nota que com as moléculas e com e com , conseguimos montar dois triângulos.
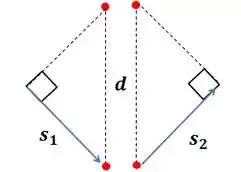
O quadrado representa um ângulo de .
Podemos também achar os ângulos internos dos triângulos em função de . Considerando que, ao refletir, os raios fazem o mesmo ângulo com os planos do cristal que o ângulo incidente, temos:
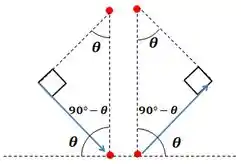
Com os triângulos retângulos, podemos então observar que:
Substituindo na diferença de fase:
Igualando à condição de interferência construtiva: