Ar a e flui em regime permanente em um secador de cabelo que consome . Por causa do tamanho da entrada de ar, a velocidade do ar na entrada é desprezível. A temperatura do ar e a velocidade na saída do secador de cabelo correspondem a e respectivamente. O escoamento do ar ocorre a uma pressão constante e de forma adiabática. Considere que o ar possui calores especifícos constantes de . Determine a vazão mássica de ar no secador de cabelo, em . Determine a vazão volumétrica de ar na saída do secador de cabelo, em .
Passo 1
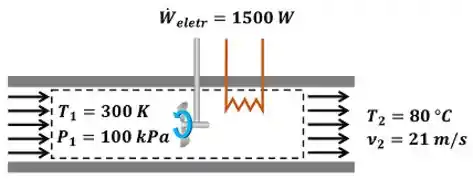
O exercício pede para a gente calcular a vazão mássica de ar que passa pelo secador de cabelo. A figura abaixo mostra todos as informações dadas pelo enunciado para calcular .
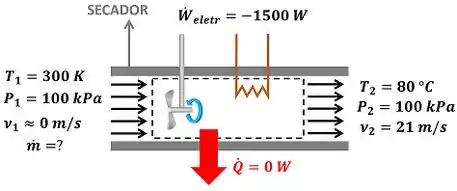
é a temperatura, é a pressão, é a velocidade do ar que está entrando no secador. é a temperatura, é a pressão, é a velocidade do ar que está saindo do secador. é a potência elétrica (taxa de trabalho elétrico) que o secador consome. Diferente da imagem do enunciado, ela é considerada negativa na resolução da questão, porque a energia está entrando no ar que passa pelo volume de controle.
A figura só mostra o valor de positivo, porque ela está mostrando apenas o módulo de .
Além disso, a questão diz que e escoamento de ar é adiabático. Isso significa que o ar não ganha nem perde calor. Ou sexa, a taxa de troca de calor entre o ar e o ambiente é nula!
Outro dado importante do enunciado é que ele diz que o escoamento do ar ocorre a pressão constante. Isso quer dizer que a pressão de entrada do ar é igual à pressão de saída do ar .
Com essas informações, podemos aprender a calcular a vazão mássica de ar .
Passo 2
pode ser calculada a partir da primeira lei da termodinâmica usada em volumes de controle em regime permanente. Como o exercício não nos informa nada sobre a energia potencial da água, concluímos que esse termo é desprezado pela questão. A energia cinética do ar entrando no secador é admitida nula, porque o enunciado diz que a velocidade de entrada é desprezível. A forma da primeira lei com todas essas considerações está abaixo.
Reorganizando a primeira lei, achamos uma fórmula para .
Ou seja, para calcular só falta aprender a calcular . No próximo passo aprenderemos a calcular !
Passo 3
Se considerarmos o ar como um gás perfeito que possui calor específico a pressão constante com valor constante, pode ser calculado com a fórmula abaixo.
onde o do ar vale:
Agora que já sabemos fazer esse cálculo, vamos começar as contas.
Passo 4
A primeira conta que precisamos fazer é para descobrir quanto vale . Para fazer esse cálculo, precisamos primeiro converter a temperatura de grau Celsius para kelvin .
Agora podemos achar o valor de . Antes de fazer isso, precisamos converter os valores de e que estão em watt para valores em quilowatt .
Além disso, é necessário dividir o termo de energia cinética do ar que está saindo do secador por mil. Isso faz o termo passar de para .
Vamos aprender no próximo passo como calcular a vazão volumétrica de saída do ar .
Passo 5
Podemos calcular a partir de , dividindo pela massa específica do ar que sai do secador .
pode ser calculado a partir da equação de gás de perfeito aplicada ao ar saindo do secador.
onde é o volume específico do ar saindo do secador e é a constante de gás do ar. Ela vale:
Agora que temos todos esses dados, vamos calcular .
Passo 6
O primeiro passo para esse cálculo é achar .
Agora podemos encontrar .