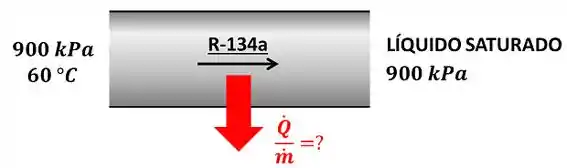
Refrigerante-134a entra no condensador de um refrigerador a e e sai como um líquido saturado à mesma pressão. Determine a transferência de calor do refrigerante por unidade de massa.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de calor por unidade de massa que a refrigerante-134a a e a perde para se transformar totalmente em líquido saturado. A figura abaixo mostra todos os dados que temos para calcular o valor de .
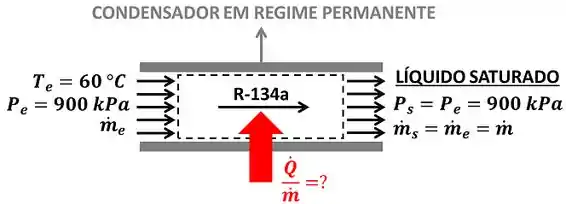
e são as vazões mássicas de entrada e saída do refrigerante-134a respectivamente e e são as pressões de entrada e saída do refrigerante-134a respectivamente. A vazão mássica de entrada é igual à vazão mássica de saída , porque o refrigerante-134a escoa em regime permanente. Ou seja, toda massa que entra no volume de controle (marcado pela linha pontilhada) tem que sair.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
Para calcular precisaremos usar a primeira lei para volumes de controle em regime permanente. O fato do enunciado não informar nada sobre a velocidade de entrada e de saída do refrigerante-134a e também não informar a altitude dessas vazões de refrigerante-134a é sinal de que a questão despreza a energia cinética e a energia potencial. Levando em conta essa simplificação, a primeira lei vira:
e são as entalpias específicas de entrada e saída do refrigerante-134a respectivamente. é a taxa de trabalho que o refrigerante-134a realiza durante o processo de condensação. Como o enunciado não fala nada sobre realização de trabalho de eixo pelo refrigerante-134a, é considerado nulo!
Por conta disso, a primeira lei vira:
No próximo passo vamos descobrir como encontrar o valor de e para poder calcular .
Passo 3
Podemos encontrar em uma tabela de saturação do refrigerante-134a como a tabela mostrada abaixo. O valor de está na mesma linha que a pressão de e na mesma coluna que !
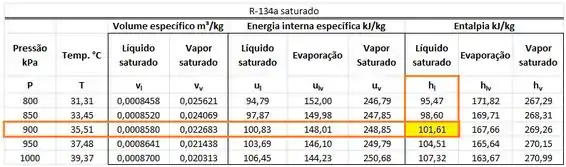
Ou seja, vale:
Podemos encontrar em uma tabela de propriedades do refrigerante-134a. A temperatura da vazão de entrada é maior que a temperatura de saturação a . Por causa disso, o R-134a entrando no condensador é um vapor superaquecido.
Por isso, achamos em uma tabela de vapor superaquecido de R-134a.
O valor de está na mesma linha que a temperatura de e na mesma coluna que .
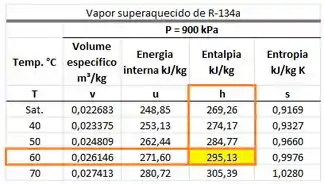
Ou seja, vale:
Agora podemos calcular .