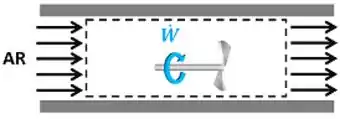
A figura abaixo mostra ar sendo ventilado através de uma tubulação. Suponha que o ar escoa em regime permanente pela tubulação e sofre trabalho de eixo do ventilador a uma taxa de . Considerando que o estado do ar que o estado do ar antes de ser ventilado é igual ao estado do ar depois de ser ventilado, calcule a taxa de calor trocado entre o ar e o ambiente. Despreze as variações de energia cinética e potencial do ar.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de calor que o ar troca com o ambiente para conseguir voltar mesmo estado que estava antes de ser ventilado. A figura abaixo mostra todos os dados que temos para calcular o valor de .
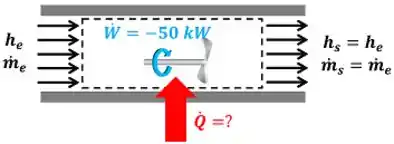
e são as vazões mássicas de entrada e saída do ar respectivamente e e são as entalpias específicas de entrada e saída do ar respectivamente. é a taxa de trabalho que o ar sofre com a ventilação. Ela é negativa, porque o ar recebe trabalho!

A entalpia de entrada é igual à entalpia de saída , porque o enunciado informa que o estado do ar que o estado do ar antes de ser ventilado é igual ao estado do ar depois de ser ventilado.

A vazão mássica de entrada é igual à vazão mássica de saída , porque o ar escoa em regime permanente. Ou seja, toda massa que entra no volume de controle (marcado pela linha pontilhada) tem que sair.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
Para calcular precisaremos usar a primeira lei para volumes de controle em regime permanente. Como o enunciado diz que a energia cinética e a energia potencial podem ser desprezadas, a primeira lei vira:
No entanto, as vazões e entalpias são iguais. Por causa disso:
Isso quer dizer que e podem ser cortados da fórmula. Com isso, a primeira lei se reduz a:
No próximo passo vamos substituir o valor de que temos na fórmula acima para calcular !