As correntes quente e fria de um fluido são misturadas em uma câmara de mistura rígida. O fluido quente flui para a câmara a uma vazão mássica de com energia de . O fluido frio flui para a câmara com uma vazão mássica de e energia de . Há transferência de calor para a vizinhança a partir da câmara de mistura a uma quantidade de . A câmara de mistura opera em regime permanente e não ganha ou perde energia ou massa com o tempo. Determine a energia transportada a partir da câmara de mistura pela mistura de fluido por unidade de massa de fluido, em .
Passo 1
Uma câmara de mistura é um equipamento que mistura duas ou mais vazões que entram nela. A figura abaixo mostra a câmara de mistura e todos os dados que o enunciado nos fornece.
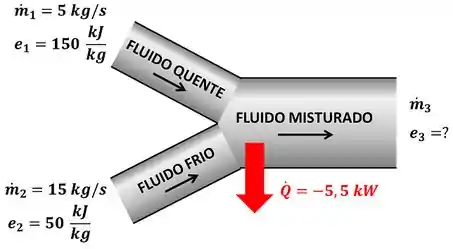
é a taxa de calor que a câmara libera para o ambiente. Ela é negativa, porque o enunciado diz que a câmara perde calor.
é a vazão mássica de fluido quente, é a vazão mássica de fluido frio e é a vazão mássica da mistura entre os fluidos quente e frio. é a energia por unidade de massa que o fluido quente carrega, é a energia por unidade de massa que o fluido frio carrega e é a energia por unidade de massa que a mistura entre os fluidos quente e frio carrega. é a incógnita do problema!

Agora vamos aprender a calcular o valor de .
Passo 2
pode ser descoberto a partir da primeira lei da termodinâmica usada em volumes de controle em regime permanente abaixo.
é a taxa de realização de trabalho do fluido.
Na fórmula acima nós vemos que a energia total por unidade de massa é a soma entre a entalpia específica , a energia cinética por unidade de massa e a energia potencial por unidade de massa . Para a gente conseguir, falta aprender a calcular e . Todos os outros termos foram dados pelo enunciado e foram mostrados pela figura.
Passo 3
Como exercício não diz em nenhum momento que o fluido realiza ou sofre trabalho de algum tipo, não existe taxa de trabalho nessa questão!
A vazão mássica da fluido misturado que está saindo as câmara é igual à soma entre as duas vazões de entrada ( e ). Essa é a fórmula de conservação de massa para volumes de controle em regime permanente.
Agora que temos todas as informações que preciamos, podemos começar os cálculos no próximo passo.
Passo 4
Iniciamos as contas encontrando o valor de .
vale: