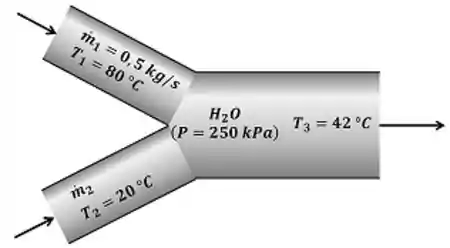
Uma corrente de água quente a entra em uma câmara de mistura com um fluxo de massa de , onde é misturada com uma corrente de água fria a . Para que a mistura saia da câmara a , determine o fluxo de massa da corrente de água fria. Considere que todas as correntes estão a uma pressão de .
Passo 1
Uma câmara de mistura é um equipamento que mistura duas ou mais vazões que entram nele. A questão pede que a gente calcule a vazão da água . A figura abaixo mostra todos os dados que o enunciado nos informa para calcular .
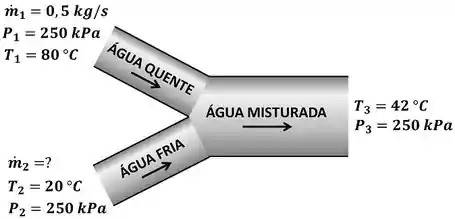
Como exercício não diz em nenhum momento que a água realiza ou sofre trabalho de algum tipo, não existe taxa de trabalho nessa questão!
O mesmo vale para ! O exercício não nos diz nada sobre troca de calor entre a água e o ambiente. Por isso, vale zero!
é a vazão mássica de água quente, é a vazão mássica de água fria e é a vazão mássica da água misturada. é a pressão e é a temperatura da água quente. é a pressão e é a temperatura da água fria. é a pressão e é a temperatura da água misturada.
Agora que entendemos o que são esses termos, vamos aprender a calcular o valor de .
Passo 2
pode ser descoberto a partir da primeira lei da termodinâmica usada em volumes de controle em regime permanente e da equação de conservação de massa. Abaixo podemos ver a primeira lei. Como o exercício não nos informa nada sobre a energia cinética e a energia potencial da água, concluímos que esses dois termos são desprezados pela questão.
é a taxa de realização de trabalho do fluido.
é a entalpia específica da água quente, é a entalpia específica da água fria e é a entalpia específica da água misturada.
pode ser caculado pela equação de conservação de massa da câmara de mistura.
Substituindo essa fórmula na primeira lei da termodinâmica, achamos:
Pra conseguir calcular só falta aprender a encontrar os valores de , e . Vamos fazer isso no próximo passo!
Passo 3
Encontramos os valores de , e a partir das tabelas de propriedades da água. O primeiro passo para decidir qual tabela usar (de saturação, de líquido comprimido ou de vapor superaquecido) é comparar as temperaturas das correntes de água (, e ) com a temperatura de saturação da água a de pressão.
Em uma tabela de saturação, vemos que a temperatura de saturação da água a vale:
Como as temperaturas (, e ) estão abaixo dessa temperatura de saturação , todas as vazões de água (quente, fria e misturada) são líquido comprimido! Por isso, temos que usar tabelas de líquido comprimido da água a . O problema é que a maioria dos livros de termodinâmica não possuem tabela de líquido comprimido para essa pressão!

No próximo passo vamos resolver esse problema!
Passo 4
Como não temos essa tabela, nós podemos considerar que a entalpia do líquido comprimido é igual à entalpia do líquido saturado na mesma temperatura! Isso quer dizer que a entalpia específica da água quente é igual à entalpia específica da água saturada à , por exemplo! Então essa entalpia está na mesma linha que e na mesma coluna que .
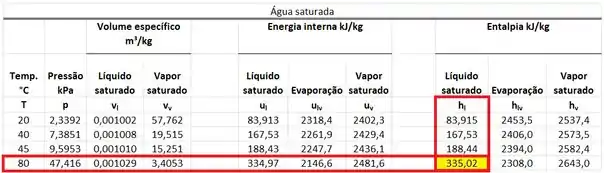
A entalpia específica da água fria está na mesma linha da temperatura de e na mesma coluna que .
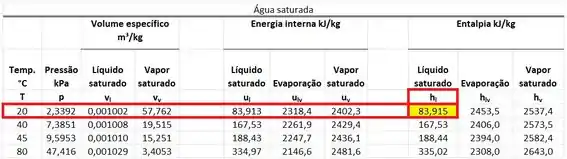
Vemos que nessa tabela não existe uma linha com de temperatura. Por isso, temos que interpolar a entalpia com as entalpias a de temperatura e a de temperatura .
Agora que temos todos esses valores podemos calcular a vazão de água fria .
Passo 5
A fórmula de se encontra abaixo.