Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Propriedades Radioativas

Ver Teoria
Exercício 41235678

Enunciado

A absortividade espectral α λ e a refletividade espectral ρ λ de um material difuso espectralmente seletivo são mostradas a seguir.

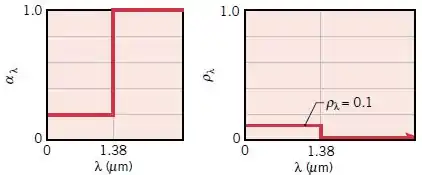
a Esboce a transmissividade espectral τ λ .

b Se a irradiação solar com G s = 750   W / m 2 e a distribuição espectral de um corpo negro a 5800   K incide sobre esse material, determine as frações da irradiação que é transmitida, que é refletida e que é absorvida pelo material.

c Se a temperatura desse material é de 350   K , determine a emissividade ε .

d Determine o fluxo térmico radiante líquido para o material.

Passo 1

a Esboce a transmissividade espectral τ λ .

A absortividade α λ , a refletividade ρ λ e a transmissividade τ λ apresentam a seguinte relação:

α λ + ρ λ + τ λ = 1

τ λ = 1 - α λ - ρ λ

Para 0 ≤ λ ≤ 1,38   μ m :

α λ = 0,2

ρ λ = 0,1

τ λ = 1 - 0,2 - 0,1 → τ λ = 0,7

Para λ ≥ 1,38   μ m :

α λ = 1

ρ λ = 0

τ λ = 1 - 1 - 0 → τ λ = 0

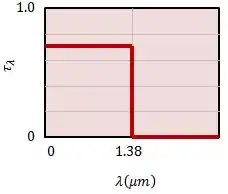
Assim, graficamente, a transmissividade será dada por:

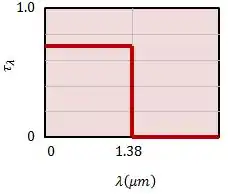
Passo 2

b Se a irradiação solar com G s = 750   W / m 2 e a distribuição espectral de um corpo negro a 5800   K incide sobre esse material, determine as frações da irradiação que é transmitida, que é refletida e que é absorvida pelo material.

A transmissividade da superfície pode ser calculada através das funções de radiação do corpo negro, onde:

τ s = τ 1 . f 0 → λ 1 + τ 2 . f λ 1 → ∞

τ s = τ 1 . f λ 1 - f 0 + τ 2 . f ∞ - f λ 1

Onde f 0 = 0 e f ∞ = 1 , logo:

τ s = τ 1 . f λ 1 - 0 + τ 2 . 1 - f λ 1

τ s = τ 1 . f λ 1 + τ 2 . 1 - f λ 1

Onde:

λ 1 . T = 1,38 × 5800 = 8000   μ m . K

f λ 1 = 0,856

Substituindo os valores:

τ s = 0,7 × 0,856 + 0 × 1 - 0,856

Passo 3

Para a refletividade, vamos fazer a mesma coisa que acabamos de fazer:

ρ s = ρ 1 . f λ 1 + ρ 2 . 1 - f λ 1

ρ s = 0 , 1 × 0,856 + 0 × 1 - 0,856

Passo 4

Para a absortividade, basta utilizar a seguinte relação:

α s + ρ s + τ s = 1

α s = 1 - ρ s - τ s

Substituindo os valores:

α s = 1 - 0,0856 - 0,599

Passo 5

c Se a temperatura desse material é de 350   K , determine a emissividade ε .

Nesse caso, precisamos definir novamente a função de radiação do corpo negro. Considerando que ε λ = α λ , teremos:

ε = α 1 . f λ 1 + α 2 . 1 - f λ 1

A função de radiação será dada por:

λ 1 . T = 1,38 × 350 = 483   μ m . K

Para esse valor, f λ 1 = 0 , logo:

ε = α 2

Passo 6

d Determine o fluxo térmico radiante líquido para o material.

O fluxo radiante será dado por:

q r a d ' ' = G s - ρ s . G s - τ s . G s - E

q r a d ' ' = α s . G s - E = α s . G s - σ . T 4

Substituindo os valores:

q r a d ' ' = 0,315 × 750 - 5,67 × 10 - 8 × 350 4

Resposta

a

b τ s = 0,599 , ρ s = 0,0856 , α s = 0,3154

c ε = 1

d q r a d ' ' = - 615   W / m 2

Exercícios de Livros Relacionados

A radiação solar incide sobre a superfície frontal de uma placa fina com componentes direto e difuso de 300 e 250 W/m², respectivamente. A radiação direta faz um ângulo de 30° com a normal da superfíc
A emissividade direcional espectral de um material difuso a 2 5 00K apresenta a seguinte distribuição:Determine a emissividade hemisférica total a 2 5 00K . Determine o poder emissivo na faixa espectr
29 – Considere a superfície difusiva do Problema 12.28. Determine a emissividade da superfície hemisférica e a potência emitida em T = 300, 500, e 700 K. Em qual comprimento de onda o pico espectral d
Uma pequena superfície de área A 1 = 5 cm2 emite radiação como um corpo negro a T 1 = 1000 K. Um sensor de radiação de área A 2 = 3 cm2 é colocado na direção normal da visualização da superfície A 1 n
A variação da transmissividade espectral de uma janela de vidro de 0,6 cm de espessura é indicada na figura a seguir. Determine a transmissividade média dessa janela para a radiação solar ( T ≈ 5.800