Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Propriedades Radioativas

Ver Teoria
Exercício 61234578

Enunciado

As variações da emissividade espectral de duas superfícies são indicadas na figura abaixo.

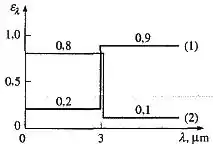
Determinar a emissividade média de cada superfície a T = 3000   K .

Além disso, determinar a absortividade e a refletividade média de cada superfície para a radiação proveniente de uma fonte a 3000   K .

Qual superfície é mais adequada para servir como um absorvedor solar?

Passo 1

Superfície (1):

A função de radiação do corpo negro será dada por:

λ 1 . T = 3 × 3000 = 9000   μ m . K → f λ 1 = 0,890029

Dessa forma, a sua emissividade média será:

ε = ε 1 . f λ 1 + ε 2 . 1 - f λ 1

ε = 0,2 × 0,890029 + 0,9 × 1 - 0,890029

ε = 0,28

Agora que encontramos a emissividade média, a absortividade média será:

α = ε

α = 0,28

Considerando as duas superfícies como opacas, τ = 0 , logo:

α + ρ = 1 → ρ = 1 - α = 1 - 0,28

ρ = 0,72

Passo 2

Superfície (2):

A função de radiação do corpo negro será dada por:

λ 1 . T = 3 × 3000 = 9000   μ m . K → f λ 1 = 0,890029

Dessa forma, a sua emissividade média será:

ε = ε 1 . f λ 1 + ε 2 . 1 - f λ 1

ε = 0 , 8 × 0,890029 + 0 , 1 × 1 - 0,890029

ε = 0 , 72

Agora que encontramos a emissividade média, a absortividade média será:

α = ε

α = 0 , 72

Considerando as duas superfícies como opacas, τ = 0 , logo:

α + ρ = 1 → ρ = 1 - α = 1 - 0 , 72

ρ = 0 , 28

Passo 3

Qual superfície é mais adequada para servir como um absorvedor solar?

A segunda superfície é mais adequada por apresentar uma maior absortividade média.

Resposta

Superfície (1):

ε = 0,28

α = 0,28

ρ = 0,72

Superfície (2):

ε = 0,72

α = 0,72

ρ = 0,28

A superfície (2) é mais adequada.

Exercícios de Livros Relacionados

A radiação solar incide sobre a superfície frontal de uma placa fina com componentes direto e difuso de 300 e 250 W/m², respectivamente. A radiação direta faz um ângulo de 30° com a normal da superfíc
A emissividade direcional espectral de um material difuso a 2 5 00K apresenta a seguinte distribuição:Determine a emissividade hemisférica total a 2 5 00K . Determine o poder emissivo na faixa espectr
29 – Considere a superfície difusiva do Problema 12.28. Determine a emissividade da superfície hemisférica e a potência emitida em T = 300, 500, e 700 K. Em qual comprimento de onda o pico espectral d
Uma pequena superfície de área A 1 = 5 cm2 emite radiação como um corpo negro a T 1 = 1000 K. Um sensor de radiação de área A 2 = 3 cm2 é colocado na direção normal da visualização da superfície A 1 n
A variação da transmissividade espectral de uma janela de vidro de 0,6 cm de espessura é indicada na figura a seguir. Determine a transmissividade média dessa janela para a radiação solar ( T ≈ 5.800