A variação da absortividade espectral de uma superfície é dada na figura abaixo.
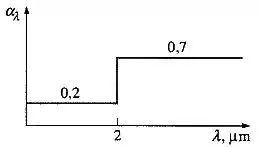
Determinar a absortividade e a refletividade média da superfície para a radiação originária de uma fonte a . Além disso, determinara a emissividade média desta superfície a .
Passo 1
A absortividade média será dada por:
Onde:
Logo:
Considerando a superfície como opaca, , logo:
Passo 2
A emissividade média será dada por:
Onde:
Logo:
Resposta
Para , .
Exercícios de Livros Relacionados
A radiação solar incide sobre a superfície frontal de uma placa fina com componentes direto e difuso de 300 e 250 W/m², respectivamente. A radiação direta faz um ângulo de 30° com a normal da superfíc
A emissividade direcional espectral de um material difuso a 2 5 00K apresenta a seguinte distribuição:Determine a emissividade hemisférica total a 2 5 00K . Determine o poder emissivo na faixa espectr
29 – Considere a superfície difusiva do Problema 12.28. Determine a emissividade da superfície hemisférica e a potência emitida em T = 300, 500, e 700 K. Em qual comprimento de onda o pico espectral d
Uma pequena superfície de área A 1 = 5 cm2 emite radiação como um corpo negro a T 1 = 1000 K. Um sensor de radiação de área A 2 = 3 cm2 é colocado na direção normal da visualização da superfície A 1 n
A variação da transmissividade espectral de uma janela de vidro de 0,6 cm de espessura é indicada na figura a seguir. Determine a transmissividade média dessa janela para a radiação solar ( T ≈ 5.800