Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra 1/3 de Simpson

Exercício 10123456789

Enunciado

Determine ∫ 1 3 4 - x - 3 2 d x

pela regra de 1/3 de Simpson com n = 8

Passo 1

A primeira coisa que costumamos fazer é calcular os subintervalos idênticos que vão dividir nossa função. Nosso h continua sendo:

h =     x 1 -   x 0 n = 3 - 1 8 = 0,25

O h determina a distância entre um intervalo e outro sempre com base no passo anterior.

Belê, mas e agora? Agora vamos montar uma tabelinha que vai nos ajudar um montão a não perder os termos de vista. Lembra da regra dos Trapézios? É, de novo isso... eu juro que é que última vez que eu pergunto isso hahahah mas é que continua sendo a mesma coisa! Então daaaale montar tabela de novo.

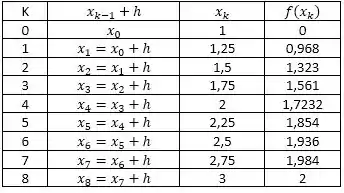
Só lembrando quando colocarmos na fórmula, par com par, ímpar com ímpar. Nossa aproximação vai ser:

∫ 1 3 4 - x - 3 2 d x ≈ h 3 f x 0 + 4 f x 1 + f x 3 + f x 5 + f x 7 + 2 f x 2 + f x 4 + f x 6 + f x 8

∫ 1 3 4 - x - 3 2 d x ≈ 0.25 3 0 + 25.468 + 9.982 + 2 = 3.121

Resposta

∫ 1 3 4 - x - 3 2 d x = 3.121