Os dados abaixo referem-se a meses de experiência de dez digitadores e o número de erros cometidos na digitação de determinado texto.

Dados:
a) Represente graficamente esse conjunto de dados.
b) Assumindo que um modelo de regressão linear é adequado, determine os coeficientes da equação pelo método dos mínimos quadrados.
c) Represente a reta de regressão no gráfico feito anteriormente
d) Qual a posição do ponto , em relação à reta de regressão?
e) Qual o número esperado de erros para um digitador com 5 meses de experiência?
Passo 1
Neste exercício temos uma amostra com n=10, e não confie nesses dados que ele dá no problema, eles estão errados, tirando o somatório de y refaça todos.
Passo 2
Para montarmos o gráfico basta pegarmos os pares (xi , yi) e ordenar no gráfico, assim:
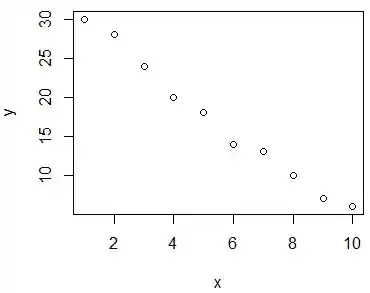
Passo 3
Para resolvermos a letra c, isto é, acharmos a reta da regressão, precisamos achar os valores de α e β, basta lembrarmos das fórmulas nos valores que calculamos na calculadora, (de novo não confia no exercício, ele fura fila no bandejão).
Aplicando os dados:
Logo a sua reta terá a cara:
Passo 4
Agora para traçar a reta pegue uns dois pontos de y na equação encontrada acima e veja que x é seu par, e trace uma reta, ficará mais ou menos assim
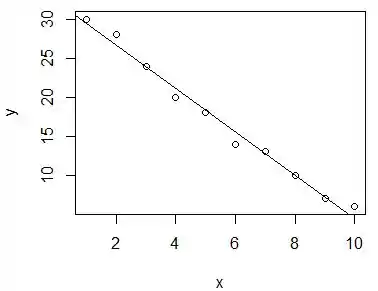
Passo 5
Para a nossa sorte já calculamos as médias amostrais, quando achamos β, logo é só achar onde fica o par (5,5,17). Uma dica o par das médias amostrais de x e y vai sempre estar sobre a reta, para provar basta aplicar o x na equação da reta e verá que o resultado será y.
Passo 6
Para resolver a letra (e), é basicamente repetir o passo que fizemos na d, mas trocando o x=5,5 para x=5.
Resposta
Ei, a resposta está no passo a passo :)