Dois especialistas e estimaram o tempo em horas a ser gasto no desenvolvimento de 11 projetos:

(a) Fazer um gráfico ramo-folha (ramo = parte inteira e folha = parte decimal) para .

(b) Calcule os três quartis para as duas variáveis e . Construa um box-plot dos dados para cada especialista. Os dois box-plots devem aparecer juntos na mesma figura, utilize a mesma escala de forma que os gráficos fiquem comparáveis. Comente os gráficos

(c) Construa um diagrama de dispersão.

(d) Se, num conjunto de n pontos no plano, existir um deles que está muito destoante do comportamento geral, qual será o efeito sobre o coeficiente de correlação de se excluir este ponto?

b)

Vamos calcular as posições dos quartis:

Agora vamos ver quem ocupa essas posições. Primeiramente para .

Os valores de em ordem crescente (não pode esquecer de botar assim!) são:

A posição é exatamente entre o e elemento, então podemos fazer uma média aritmética entre eles pra descobrir quem é :

A posição nos dá a mediana:

A posição é exatamente entre o e elemento, então podemos fazer uma média aritmética entre eles pra descobrir quem é :

O vai ser:

E as cercas:

Então o menor valor não discrepante vai ser:

E o maior não discrepante:

E vamos ter um valor discrepante! O que é maior que nossa cerca superior.

Agora para . Os valores em ordem crescente são:

A posição é exatamente entre o e elemento, mas aqui eles dois valem , então sabemos que a média também vai valer isso. Então:

A posição nos dá a mediana:

A posição é exatamente entre o e elemento, então podemos fazer uma média aritmética entre eles pra descobrir quem é :

O vai ser:

E as cercas:

Então o menor valor não discrepante vai ser:

E o maior não discrepante:

E vamos ter um valor discrepante! O que é menor que nossa cerca inferior.

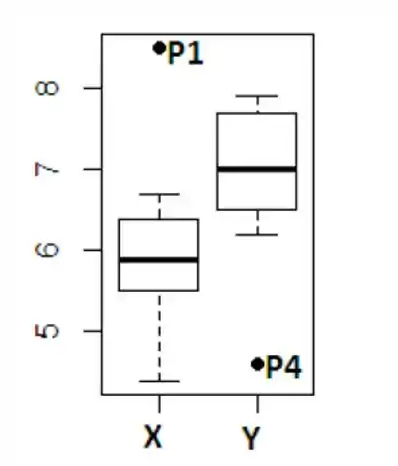
Com as informações que temos, já podemos montar os dois Box-Plots pedidos:

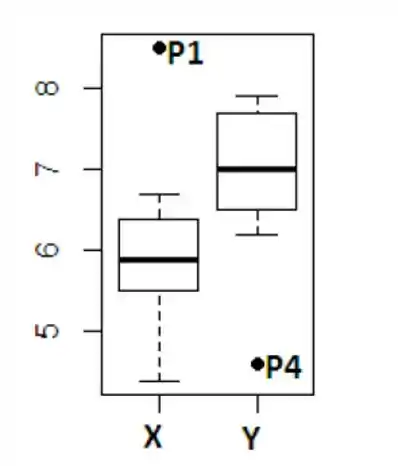
Podemos notar que as duas variáveis possuem valores discrepantes, o para mais e o para menos. Os valores não discrepantes de são praticamente simétricos, enquanto os não discrepantes de possuem maior assimetria.

c)

Para o diagrama de dispersão, primeiro vamos olhar pra tabela dada:

Com esses dados, podemos desenhar dois eixos, e , representar os valores de e neles e cruzar os dados respectivos ao mesmo projeto. Ficamos dois eixos coordenados e vários pontinhos representando o cruzamento de dados.

Daí observamos o comportamento desses pontinhos. Concorda comigo que eles tão meio que crescentes e tem um carinha lá embaixo meio isolado (quando e )?

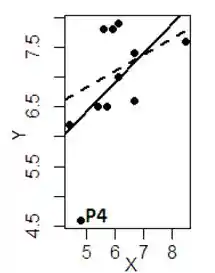
Vamos traçar uma reta crescente que seja uma aproximação da regressão desses pontos então, e também podemos identificar o pontinho isolado, que acaba fugindo muito da reta, como um ponto discrepante . Ficaríamos com isso aqui:

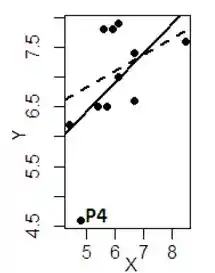
Nós até poderíamos calcular a expressão certinha dessa reta lááá pelo método da regressão linear, mas como aqui só foi pedido o diagrama de dispersão, não precisamos de valores exatos na representação, mas sim uma boa identificação da tendência do nosso gráfico.

d)

Concorda comigo que um ponto destoante é como se fosse um peso morto que fica querendo desequilibrar os outros dados que tão juntinhos de boas? Então, se a gente retirar o diferentão, o comportamento dos outros dados juntinhos vai ser mais respeitado, porque tiramos o peso morto!

E como agora todos eles vão estar próximos sem ninguém tentando puxá-los pra outro canto, vai ser mais fácil pra gente aproximar esses caras a uma reta.

Mas lembra que quando temos um coeficiente de correlação igual a ou é quando temos uma relação linear perfeita entre os dados (decrescente e crescente)? Então, quanto mais próximo um coeficiente de correlação for de , mais próximo o gráfico é de uma reta.

Podemos dizer então que, retirando um ponto destoante do gráfico, vai sempre ser mais simples linearizar os outros pontos, ou seja, sempre vamos aumentar o valor do coeficiente de correlação em módulo.