Considere os autovalores e , e seus respectivos autovetores e de uma matriz .
Determine um sistema de equações diferenciais .
Esboce um retrato do sistema.
Esboce a trajetória que passa pelo ponto .
Passo 1
Determine um sistema de equações diferenciais .
Cara, temos que lembrar o seguinte:
Onde é matriz dos autovetores normalizados nas colunas e é uma matriz diagonal, na qual a sua diagonal é cada autovalor da matriz .
Passo 2
Então, vamos montar cada matriz dessa e encontrar quem é :
Agora, para encontrar , precisamos normalizar os autovetores:
Passo 3
Normalizando
Passo 4
Encontrando
Lembrando que como colocamos o no primeiro termo da diagonal, a primeira coluna tem que ser o autovetor associado a ele, e assim respectivamente.
Passo 5
Para encontrar , basta inverter a matriz. Lembrando que para inverter uma matriz :
Então:
Passo 6
Calculando :
Passo 7
Esboce um retrato do sistema.
Bom, a gente está lidando com um sistema que tem a seguinte solução:
Se , as soluções serão paralelas a , então o retrato de fase pode ser o seguinte:
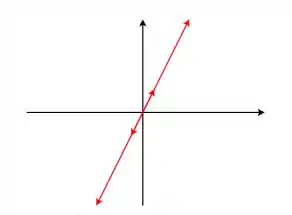
Pode ser qualquer translação dessa reta também.
Se , as soluções serão paralelas a , então o retrato de fase pode ser o seguinte:
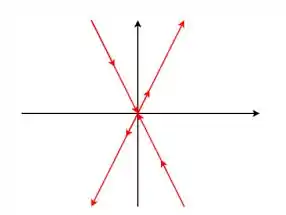
Como o autovalor é negativo, ele se torna um atrator, enquanto que o autovalor positivo torna o autovetor correspondente um repulsor.
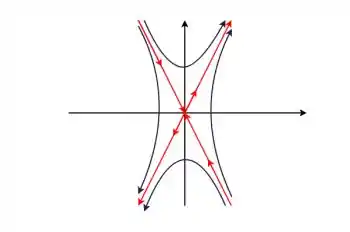
Cara, caso ambas as constantes sejam diferentes de , pra olhar o retrato do sistema, basta olharmos para os autovetores e autovalores. Como os autovalores são reais e diferentes e com sinais diferentes, nosso retrato será hiperbolítica:
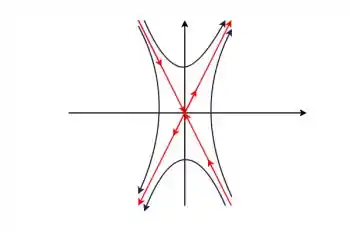
Veja bem: conforme , a solução se aproxima de e conforme , a solução se aproxima de .
Passo 8
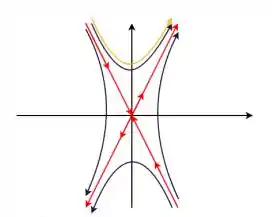
Esboce a trajetória que passa pelo ponto .
Amigx, naquele ponto especificado, a trajetória vai ser hiperbólica, porque esse ponto está acima do vetor . A trajetória está em amarelo.
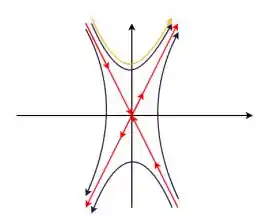
Resposta